datetime:2023/09/25 10:22
author:nzb
该项目来源于大佬的动手学ROS2
2.空间坐标描述实战
上一节我们学习了坐标描述和坐标变换的理论知识,本节课我们把重点放到动手实现上,通过numpy实现坐标的描述和变换,同时结合ROS2鱼RVIZ进行坐标关系可视化与求解。
通过本节你将掌握:
- 使用numpy表示位置矢量和旋转矩阵
- 使用numpy进行平移与旋转坐标变换
- 了解ROS2中TF2的概念
- 使用tf2相关CLI工具进行坐标变换
- 使用python操作TF进行坐标变换
1.numpy表示位姿
在前几节中,带你安装使用了ROS2和MiniConda,并学习使用Numpy进行矩阵相关运算的验证。
那我们如何使用numpy中的矩阵表示位置矢量和旋转矩阵呢?
1.1 位置表示
上一节中我们使用一个3行1列的矩阵表示了位置,那么我们在numpy中自然也可以使用这样一个矩阵表示。
打开终端,输入下面指令打开jupyter
jupyter-notebook
新建一个python3的代码并重命名,接着在单元格中导入numpy
import numpy as np

1.1.1 位置矩阵
使用3*1的矩阵表示位置,我们新建一个沿着x、y、z各平移1个单位的位置矢量。
np.asarray([1.0,1.0,1.0]).reshape(3,1)
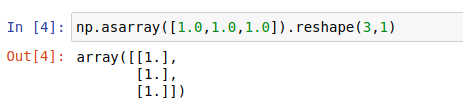
1.2 姿态表示
姿态可以使用3*3的旋转矩阵表示,3*3的单位矩阵代表没有姿态变换,注意没有姿态变换不是零矩阵,而是单位矩阵。
我们新建一个旋转矩阵,用该旋转矩阵表示绕着z轴旋转45度,可以这样写:
import math
import numpy as np
theta = math.radians(45)
R_AB = np.asarray([math.cos(theta),-math.sin(theta),0,
math.sin(theta),math.cos(theta),0,
0,0,1
]).reshape(3,3)
print(R_AB)
运行后得到的旋转矩阵是不是和上节的一样
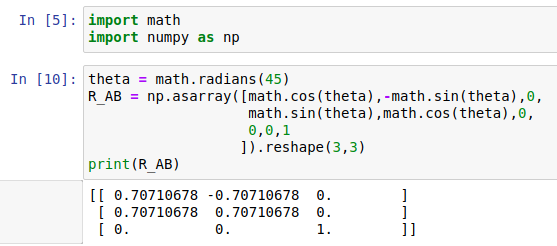
2.numpy坐标变换
掌握了使用numpy表示位置和姿态后,接着我们使用numpy来完成上一节的小练习
2.1 题目
如图🔓示,已知:

1.相机坐标系{C}为参考坐标系,工具坐标系{P}的位置矢量在相机坐标系{C}的x,y,z各轴投影为 ,并且工具坐标系和相机坐标系姿态相同。
2.机器人基坐标系{B}为参考坐标系,相机坐标系{C}的位置矢量在{B}各轴的投影为 ,坐标系{C}绕着坐标系{B}的x轴转了180度
可以参考下图看题目
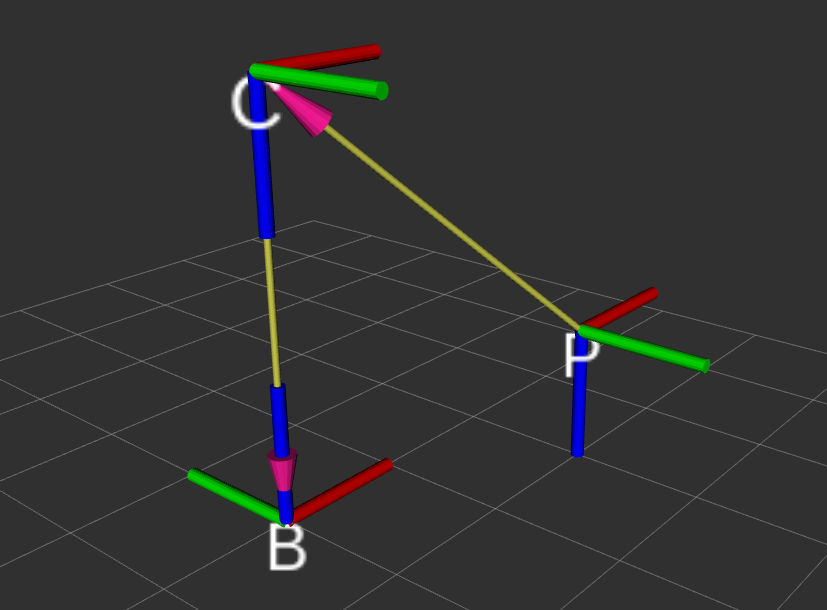
求:
{B}为参考坐标系,坐标系{P}的位置矢量和旋转矩阵
2.2 使用numpy求解
2.2.1 旋转矩阵求解
这里我们就需要使用复合坐标变换了,根据坐标变换规则有:
{C}和{P}姿态相同,所以 是一个单位矩阵。又因为{C}绕着{B}的x旋转了180度,根据上节的重要公式2可知
所以 对应的程序可以这样写
import math
import numpy as np
theta = math.radians(180)
R_BC = np.asarray([1, 0, 0,
0, math.cos(theta), -math.sin(theta),
0, math.sin(theta), math.cos(theta)]).reshape(3, 3)
所以 可以用程序求得:
R_BP = R_BC*np.identity(3)
print("旋转矩阵R_BP:\n",R_BP)
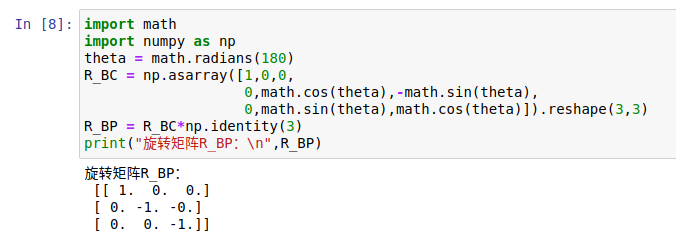
2.2.2 平移矩阵求解
根据复合变换规则可知:
根据描述有:
、
所以可以写这样写程序:
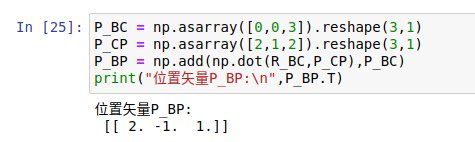
P_BC = np.asarray([0, 0, 3]).reshape(3, 1)
P_CP = np.asarray([2, 1, 2]).reshape(3, 1)
P_BP = np.add(np.dot(R_BC, P_CP), P_BC)
print("位置矢量P_BP:\n", P_BP.T)
运行下,可以得到结果
2.3 结果对比
与上节课答案一致
位置矢量:
旋转矩阵: