datetime:2020/8/1 13:28
author:nzb
numpy基础
numpy用于数组计算
中文文档
import numpy as np
import random
创建数组
a1 = np.array([1,2,3])
a2 = np.array(range(5))
a3 = np.arange(8)
a4 = np.array(range(4), dtype='f4')
a5 = np.array([1,0,1,0,1,0], dtype=bool)
print(a1, a2, a3, sep='\n')
print(type(a1), type(a2), type(a3))
print("a3:dtype:", a3.dtype)
print("a4:dtype:", a4.dtype)
print("a5:dtype:", a5.dtype)
print("a1调整dtype前",a1.dtype )
a1 = a1.astype('float32')
print("a1调整dtype后",a1.dtype )
print("\n")
a6 = np.array([random.random() for _ in range(10)])
print(a6)
print(np.round(a6, 3))
[1 2 3]
[0 1 2 3 4]
[0 1 2 3 4 5 6 7]
<class 'numpy.ndarray'> <class 'numpy.ndarray'> <class 'numpy.ndarray'>
a3:dtype: int32
a4:dtype: float32
a5:dtype: bool
a1调整dtype前 int32
a1调整dtype后 float32
[0.67067085 0.2306847 0.25868171 0.71041073 0.53141459 0.40654488
0.62679249 0.51855766 0.30907571 0.63072732]
[0.671 0.231 0.259 0.71 0.531 0.407 0.627 0.519 0.309 0.631]
数据类型

形状
a7 = np.array([[1,2,3],[4,5,6]])
a8 = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[4,5,6]] ])
print(a3, a7, a8, sep='\n')
print(a3.shape, a7.shape, a8.shape)
[0 1 2 3 4 5 6 7]
[[1 2 3]
[4 5 6]]
[[[1 2 3]
[4 5 6]]
[[7 8 9]
[4 5 6]]]
(8,) (2, 3) (2, 2, 3)
a9 = np.arange(12)
print(a9.reshape((3,4)), a9.reshape((2,6)), a9.reshape((2,2,3)), a9.reshape((2,3,2)), sep='\n\n\n')
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
[[[ 0 1 2]
[ 3 4 5]]
[[ 6 7 8]
[ 9 10 11]]]
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]]
print(a9.reshape((12,)),a9.reshape((1,12)), a9.reshape((12,1)), sep='\n\n\n')
[ 0 1 2 3 4 5 6 7 8 9 10 11]
[[ 0 1 2 3 4 5 6 7 8 9 10 11]]
[[ 0]
[ 1]
[ 2]
[ 3]
[ 4]
[ 5]
[ 6]
[ 7]
[ 8]
[ 9]
[10]
[11]]
a10 = np.arange(12).reshape((2,2,3))
print(a10, a10.flatten(), sep='\n\n\n')
[[[ 0 1 2]
[ 3 4 5]]
[[ 6 7 8]
[ 9 10 11]]]
[ 0 1 2 3 4 5 6 7 8 9 10 11]
计算
a11 = np.arange(12).reshape((3,-1))
print(a11, a11/2, a11/0, sep='\n\n\n')
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[0. 0.5 1. 1.5]
[2. 2.5 3. 3.5]
[4. 4.5 5. 5.5]]
[[nan inf inf inf]
[inf inf inf inf]
[inf inf inf inf]]
C:\Users\Admin\Anaconda3\lib\site-packages\ipykernel_launcher.py:4: RuntimeWarning: divide by zero encountered in true_divide
after removing the cwd from sys.path.
C:\Users\Admin\Anaconda3\lib\site-packages\ipykernel_launcher.py:4: RuntimeWarning: invalid value encountered in true_divide
after removing the cwd from sys.path.
维度相同
a12 = np.arange(1,13).reshape((3,4))
a13 = np.arange(11, 23).reshape((3,4))
print(a12, a13, sep='\n'*3)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[11 12 13 14]
[15 16 17 18]
[19 20 21 22]]
print("加:", a12 + a13, end="\n"*3)
print("减:", a12 - a13, end="\n"*3)
print("乘:", a12 * a13, end="\n"*3)
print("除:", a12 / a13, end="\n"*3)
加: [[12 14 16 18]
[20 22 24 26]
[28 30 32 34]]
减: [[-10 -10 -10 -10]
[-10 -10 -10 -10]
[-10 -10 -10 -10]]
乘: [[ 11 24 39 56]
[ 75 96 119 144]
[171 200 231 264]]
除: [[0.09090909 0.16666667 0.23076923 0.28571429]
[0.33333333 0.375 0.41176471 0.44444444]
[0.47368421 0.5 0.52380952 0.54545455]]
维度不相同
- 需要有一个维度的相同
- 广播原则
- 如果两个数组的后缘维度(即从末尾开始算起的维度)的轴长度相符或其中一方的长度为1,则认为它们是广播兼容的,广播会在缺失和(或)长度为1的维度上进行
a14 = np.arange(6)
a15 = np.arange(24).reshape((4,6))
a16 = np.arange(4).reshape((4,1))
a17 = np.arange(10)
print(a14, a15, a16, a17, sep="\n"*3)
[0 1 2 3 4 5]
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
[[0]
[1]
[2]
[3]]
[0 1 2 3 4 5 6 7 8 9]
print(a15-a14, a15-a16, sep='\n'*3)
[[ 0 0 0 0 0 0]
[ 6 6 6 6 6 6]
[12 12 12 12 12 12]
[18 18 18 18 18 18]]
[[ 0 1 2 3 4 5]
[ 5 6 7 8 9 10]
[10 11 12 13 14 15]
[15 16 17 18 19 20]]
print(a15-a14, a15-a16, a15-a17, sep='\n'*3)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-16-3ad53f5deac4> in <module>
1 # 维度不一样时会计算对应位置不一样也不一定可以计算
----> 2 print(a15-a14, a15-a16, a15-a17, sep='\n'*3)
ValueError: operands could not be broadcast together with shapes (4,6) (10,)
轴
- 二维
- axis=0:行
- axis=1:列

- 三维
- axis=0:行
- aixs=1:列(每一行的每一列)
- aixs=2:块(每一行的每一列的每个元素)
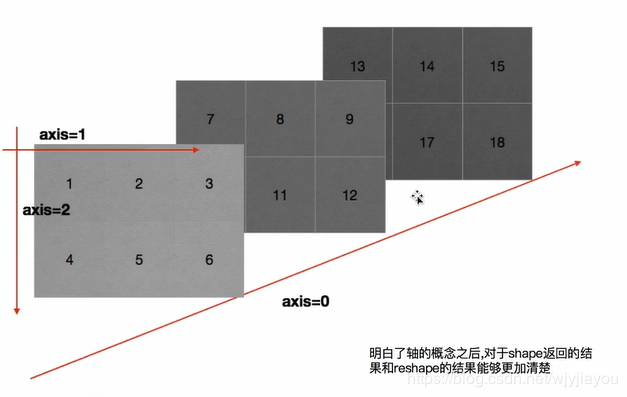
print(a10, np.sum(a10, axis=0), np.sum(a10, axis=1), np.sum(a10, axis=2), sep='\n'*3)
[[[ 0 1 2]
[ 3 4 5]]
[[ 6 7 8]
[ 9 10 11]]]
[[ 6 8 10]
[12 14 16]]
[[ 3 5 7]
[15 17 19]]
[[ 3 12]
[21 30]]
转置
a18 = np.arange(24).reshape((4,6))
print(a18, a18.transpose(), a18.T, a18.swapaxes(1,0), sep='\n'*3)
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
[[ 0 6 12 18]
[ 1 7 13 19]
[ 2 8 14 20]
[ 3 9 15 21]
[ 4 10 16 22]
[ 5 11 17 23]]
[[ 0 6 12 18]
[ 1 7 13 19]
[ 2 8 14 20]
[ 3 9 15 21]
[ 4 10 16 22]
[ 5 11 17 23]]
[[ 0 6 12 18]
[ 1 7 13 19]
[ 2 8 14 20]
[ 3 9 15 21]
[ 4 10 16 22]
[ 5 11 17 23]]
索引与切片
中文文档
print(a2, a2[0], a2[2:5],a2[::-1], sep='\n'*2)
[0 1 2 3 4]
0
[2 3 4]
[4 3 2 1 0]
三个点( ... )表示产生完整索引元组所需的冒号。例如,如果 x 是rank为5的数组(即,它具有5个轴),则:
x[1,2,...] 相当于 x[1,2,:,:,:]x[...,3] 等效于 x[:,:,:,:,3]x[4,...,5,:] 等效于 x[4,:,:,5,:]
print("二维",a12,a12[:2,:2], a12[:, 1:3],a12[[0, 1,2],[1,2,0]], sep='\n'*2)
print("三维",a10, a10[:,:2,:2], a10[1,...],sep='\n'*3)
二维
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[1 2]
[5 6]]
[[ 2 3]
[ 6 7]
[10 11]]
[2 7 9]
三维
[[[ 0 1 2]
[ 3 4 5]]
[[ 6 7 8]
[ 9 10 11]]]
[[[ 0 1]
[ 3 4]]
[[ 6 7]
[ 9 10]]]
[[ 6 7 8]
[ 9 10 11]]
index = np.where(a12 < 5)
print(a12,index, a12[index] ,sep='\n'*2)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
(array([0, 0, 0, 0], dtype=int64), array([0, 1, 2, 3], dtype=int64))
[1 2 3 4]
print(np.where(a12 < 5, 1, 0))
[[1 1 1 1]
[0 0 0 0]
[0 0 0 0]]
数据拼接
a1 = np.arange(12).reshape((2,6))
a2 = np.arange(12, 24).reshape((2,6))
a3 = np.vstack((a1, a2))
a4 = np.hstack((a1, a2))
print(a3, a4, sep="\n"*3)
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
[[ 0 1 2 3 4 5 12 13 14 15 16 17]
[ 6 7 8 9 10 11 18 19 20 21 22 23]]
行列交换
a3
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
a3[[1,2], :] = a3[[2,1], :]
print("行交换",a3, sep='\n')
a3[:, [0,2]] = a3[:,[2,0]]
print("行交换",a3, sep='\n')
行交换
[[ 0 1 2 3 4 5]
[12 13 14 15 16 17]
[ 6 7 8 9 10 11]
[18 19 20 21 22 23]]
行交换
[[ 2 1 0 3 4 5]
[14 13 12 15 16 17]
[ 8 7 6 9 10 11]
[20 19 18 21 22 23]]
import matplotlib.pyplot as plt
%matplotlib inline
a1 = np.random.rand(100)
plt.scatter(range(100), a1)
plt.show()
nan和inf
print(type(np.nan),np.nan == np.nan, np.nan is np.nan, sep="\n"*2)
<class 'float'>
False
True
a1 = np.array([1,2,np.nan])
print(a1 != a1, np.count_nonzero(a1 != a1), sep="\n")
print(np.isnan(a1))
print("求和:", np.sum(a1))
a1[np.isnan(a1)]=0
print(a1)
[False False True]
1
[False False True]
求和: nan
[1. 2. 0.]
np.isnan(a1)
array([False, False, False])
a1 = np.array([1,2,np.nan])
a2 = np.arange(12).reshape((3,4)).astype("float")
a2[[1], 2:] = np.nan
a = np.array([np.nan, 1,2,np.nan,3,4,5])
print (a[~np.isnan(a)])
[1. 2. 3. 4. 5.]



