datetime:2024/3/05 14:31
author:nzb
有序表
- 红黑树(平衡搜索二叉树BST)
- AVL树(平衡搜索二叉树BST)
- SB树(平衡搜索二叉树BST),比较好改
- 跳表(单链表)
搜索二叉树
构造
- 通过新建节点,大于头节点放右边,小于放左边,暂时不考虑平衡性。直至放下
- 一般默认搜索二叉树是没有重复的节点的,如果有重复数据,可以在每个节点加功能项,比如计数或字符串数组保存相关信息
查找:找小于等于6离它最近的
4
/ \
2 8
\ /\
3 7 9
/
5
首先来到头结点,4 < 6, 变量记录下ans=4,左树都比4小,只能在右树找
来到8, 8>6, 8的右树肯定都比6大,所以来到左树
来到7, 7>6
来到5, 5<6, ans=5, 那5的右树还有没有小于等于6的呢,5没有右树了,所以最后ans=5
- 删除:删除前需要先查找
- 删除的节点没有左右孩子,直接删(找到当前节点,记下父节点,然后把父节点指为空)
- 删除的节点左右孩子不双全(直接把父节点指向孩子)
- 删除的节点都有左右孩子:可以用左树最右节点代替或者右树最左节点代替
...
/
3
/ \
2 7
/ \ /\
1 2.5 6 ...
/ \...
4
\...
假如需要删除3,3上面还有节点
可以用左树最右节点代替或者右树最左节点代替
比如:用4替代
4剥离出来,4的右孩子给6,6的左树指向4的右孩子(因为4是6的左树,所以4的右树也小于6)
然后把4替换到3
...
/
4
/ \
2 7
/ \ /\
1 2.5 6 ...
/ \...
/...
- 红黑树,AVL树,SB树的增删改查都是以上这些
- 上面的操作没有平衡性,做不到
O(logN),比如用户给1,2,3,4,5,6就变成O(N),棒状结构,查的时候就像单链表一样
1
\
2
\
3
\
4
\
...
何为具有平衡性的树?
狭义的平衡二叉树需要节点的左右高度差小于等于1
广义可以是左右数节点相差不大或者左右树高度相差不大即可
- 树的左旋:头节点倒向左边
①:节点
⑴:子树
①
/ \
② ③
/ \ / \
⑷ ⑸ ⑹ ⑺
①左旋后
③
/ \
① ⑺
/ \
② ⑹
/ \
⑷ ⑸
反过来③右旋后是不是变回去,平衡了
- 树的右旋:头节点导向右边
①:节点
⑴:子树
①
/ \
② ③
/ \ / \
⑷ ⑸ ⑹ ⑺
①右旋后
②
/ \
⑷ ①
/ \
⑸ ③
/ \
⑹ ⑺
反过来②左旋后是不是变回去,平衡了
——————————————————————————————————————
| |
| |
| ————————————————————————— |
| | | |
| | | |
| | ————————— | |
| | | 搜索 | | |
| | | 二叉树 | | |
| | | | | |
| | ————————— | |
| | 有左旋右旋的操作 | |
| | | |
| ————————————————————————— |
| AVL树/红黑树/SB树 |
| |
——————————————————————————————————————
- 首先是搜索二叉树,其次提供了左旋右旋的操作,在此基础上每颗树根据自己的平衡标准,利用左旋右旋做平衡
AVL树
- 增加,删除导致不平衡
- 其为狭义平衡化
- 增删改查就是上面的搜索二叉树的操作
- 增加操作后,检查时机,会往上查一下每个节点是否有平衡性
- 删除操作后,检查时机,会往上查一下每个节点是否有平衡性
- 但有个特殊情况,就是如果节点有左右孩子,应该从哪里开始查,比如上面删除3,就要从6开始查
具体如何看平衡性被破坏
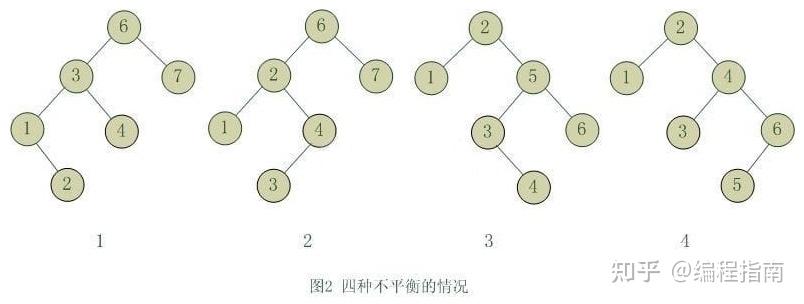
- 6节点的左子树3节点高度比右子树7节点大2,左子树3节点的左子树1节点高度大于右子树4节点,这种情况成为左左(LL)(左孩子的左子树深度大), 右旋调整。
- 6节点的左子树2节点高度比右子树7节点大2,左子树2节点的左子树1节点高度小于右子树4节点,这种情况成为左右(LR)。
- 保持平衡性:想办法让4做头部,步骤: 2节点左旋,然后4节点右旋
- 2节点的左子树1节点高度比右子树5节点小2,右子树5节点的左子树3节点高度大于右子树6节点,这种情况成为右左(RL)。
- 保持平衡性:想办法让3做头部,步骤:5节点右旋,然后3节点左旋
2节点的左子树1节点高度比右子树4节点小2,右子树4节点的左子树3节点高度小于右子树6节点,这种情况成为右右(RR),左旋调整。
往上调整时间复杂度:往上走的节点数
log(N)个,每个节点调整代价O(1),所以时间复杂度为O(logN)
如何判断是什么类型
// 检查调整函数
private void rebalance(AVLNode node) {
while (node != null) {
Node parent = node.parent;
int leftHeight = (node.left == null) ? -1 : ((AVLNode) node.left).height;
int rightHeight = (node.right == null) ? -1 : ((AVLNode) node.right).height;
int nodeBalance = rightHeight - leftHeight;
// rebalance (-2 means left subtree outgrow, 2 means right subtree)
if (nodeBalance == 2) { // 右树比左树高
if (node.right.right != null) { // RR型
node = (AVLNode)avlRotateLeft(node); // 内部有更新高度
break;
} else { // RL型
node = (AVLNode)doubleRotateRightLeft(node); // 内部有更新高度
break;
}
} else if (nodeBalance == -2) {
if (node.left.left != null) { // LL型
node = (AVLNode)avlRotateRight(node); // 内部有更新高度
break;
} else { // LR型
node = (AVLNode)doubleRotateLeftRight(node); // 内部有更新高度
break;
}
} else {
updateHeight(node); // 更新高度,插入或删除时平衡性没破坏,但是也要更新高度
}
node = (AVLNode)parent; //往上走
}
}
介绍SB树及其实现
平衡性
每棵子树的大小,不小于其兄弟的子树大小,既每棵叔叔树的大小,不小于其任何侄子树的大小
A
/ \
B C
/ \ /\
D E F G
/\ /\ /\ /\
...............
[B] >= max([F], [G])
[C] >= max([D], [E])
跟AVL树一样有4种类型,LL, LR, RR, RL
具体实现与调整细节
LL:左孩子的左孩子的大小比右孩子大
L R 是节点,A B C D 都是子树
T
/ \
L R
/ \ /\
A B C D
假设来到T, 它的平衡性被破坏了,是因为 [A] >= [R]
它的调整过程叫m(T), m(T)有以下构成
1、先做右旋
L
/ \
A T
/\
B R
/\
C D
2、往下检查哪个节点孩子变了,T变化了,执行m(T)继续递归
3、往下检查哪个节点孩子变了,L变化了,执行m(L)继续递归
RR:右孩子的右孩子的大小比左孩子大,即[D] > [A],调整跟LL类似,先左旋,继续递归LR:左孩子的右孩子的大小比左孩子大,[B] > [R]
L R B是节点,A C D E F 都是子树
T
/ \
L R
/ \ /\
A B C D
/ \
E F
调整 m(T),调整步骤如下
1、L左旋
2、T右旋
3、谁的孩子变化了,递归m(L)
4、谁的孩子变化了,递归m(T)
5、谁的孩子变化了,递归m(B)
和AVL树一样,想办法把B改为大头部
B左旋,再右旋
B
/ \
L T
/ \ / \
A E F R
/ \
C D
// 检查调整函数
private SBTNode<K, V> matain(SBTNode<K, V> cur) {
if (cur == null) {
return null;
}
if (cur.l != null && cur.l.l != null && cur.r != null && cur.l.l.size > cur.r.size) { // LL型
cur = rightRotate(cur);
cur.r = matain(cur.r);
cur = matain(cur);
} else if (cur.l != null && cur.l.r != null && cur.r != null && cur.l.r.size > cur.r.size) { // LR
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
cur.l = matain(cur.l);
cur.r = matain(cur.r);
cur = matain(cur);
} else if (cur.r != null && cur.r.r != null && cur.l != null && cur.r.r.size > cur.l.size) { // RR
cur = leftRotate(cur);
cur.l = matain(cur.l);
cur = matain(cur);
} else if (cur.r != null && cur.r.l != null && cur.l != null && cur.r.l.size > cur.l.size) { // RL
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
cur.l = matain(cur.l);
cur.r = matain(cur.r);
cur = matain(cur);
}
return cur;
}
红黑树
最复杂, 现在不怎么用,SB树和AVL树比它好,面试官要你手撕,怼他
- 平衡标准
- 新增操作:标准为5个情况
- 删除操作:标准为8个情况
- 平衡标准是什么
- 每个节点不是红就是黑
- 头结点和叶节点(最底层的空节点,不是没有左右孩子的节点),必须为黑
- 任何2个红节点不能相邻
- 最重要一点:对于任何一个子树来说,从cur当前头部到它叶节点的每一条路径,要求黑节点数量一样
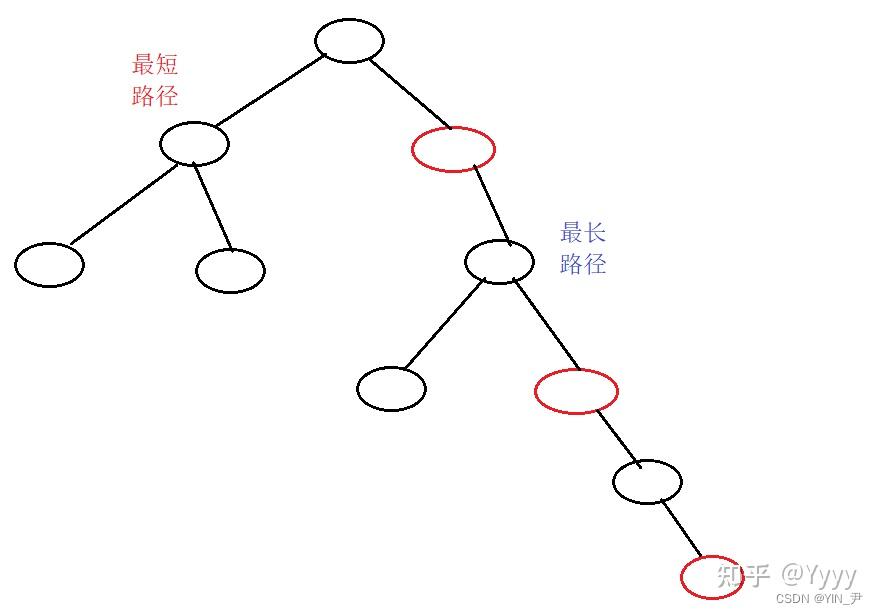
- 如果我从一个节点出发,往下走,怎么样最长,那一定是:红->黑->红->黑...交替
- 最短的路就是全黑
当然实际中不同的红黑树情况是不一样的,所以我们这里来分析一种极端的情况: 大家想,如果一棵红黑树有红有黑,它里面如果有一条全黑的路径,那这条全黑的路径一定就是最短路径; 如果有一条是一黑一红,一黑一红...,这样黑红相间的,那他就是最长的路径。 然后它们里面的黑色结点个数又是相同的的,所以最长路径最多是最短路径的两倍,不可能超过最短路径两倍。 所以这样红黑树的高度就能够保持在一个相对平衡的范围内,当然他就没有AVL树那么严格
介绍SkipList及其实现
跳表有着和红黑树、SBT树相同的功能,都能实现在O(log(N))内实现对数据的增删改查操作。但跳表不是以二叉树为原型的
- 平衡性:
- 利用随机函数打破输入规律
- 具体实现与调整细节
记该结构为SkipList,该结构中可以包含有很多结点(SkipListNode),每个结点代表一个被添加到该结构的数据项。 当实例化SkipList时,该对象就会自带一个SkipListNode
(不代表任何数据项的头结点)。
public static class SkipListNode<K extends Comparable<K>, V> {
public K key;
public V val;
public ArrayList<SkipListNode<K, V>> nextNodes;
public SkipListNode(K k, V v) {
key = k;
val = v;
nextNodes = new ArrayList<SkipListNode<K, V>>();
}
- 刚开始有一个默认节点,该
key是全局最小(无穷小),用户给的任何数据都没他小,有一条往外指向空的指针 - 添加数据
- 当你向其中添加数据之前,首先会抛硬币,将第一次出现正面朝上时硬币被抛出的次数作为该数据的层数(
level,最小为1), 接着将数据和其层数封装成一个SkipListNode添加到SkipList中,其他节点抛完硬币就不会再变了 结构初始化时,其头结点的层数为0,但每次添加数据后都会更新头结点(默认节点)的层数为所添数据中层数最大的。
- 当你向其中添加数据之前,首先会抛硬币,将第一次出现正面朝上时硬币被抛出的次数作为该数据的层数(
例子1
3-> 3->
2-> 2-> 2->
1-> 1-> 1-> 1->
0-> 0-> 0-> 0->
默认 3 4 5
来了一个4,层数为2层,如何加进去
默认不需要扩充,永远从最高层开始
最高层开始找到小于等于4最右的节点(默认节点),也就找到大于4最左的节点(5)
但是4没有到第三层,什么也不做,默认节点本层往下跳,来到第二层
找到小于等于4的最右节点(3节点)
但是4没有到第二层,什么也不做,3节点本层往下跳,来到第一层
找到小于等于4的最右节点(3节点)
4有一层,则3节点的第一层指向4,4的第一层指向5,3节点继续往下跳,来到第零层
找到小于等于4的最右节点(3节点)
4有第零层,则3节点的第零层指向4,4的第零层指向5,结束
例子2
5---------------------->5---------------------->5->
4---------------------->4---------------->4---->4->
3---------------->3---->3---------->3---->3---->3->
2---->2---------->2---->2---------->2---->2---->2->
1---->1---->1---->1---->1---------->1---->1---->1->
0---->0---->0---->0---->0---->0---->0---->0---->0->
默认 3 10 15 20 30 40 50 100
- 增加节点
假设加入2层的70
默认节点,不用扩充,永远从最高层第5层开始,找到小于等于70的节点(20节点第5层),加速一下子把3,10,15跨过去了,但是70没有第5层,往下跳
来到20第4层,找到小于等于70的节点(50节点第4层),加速跨过去30,40,但是70没有第4层,往下跳
50来到第3层,找到小于等于70的节点(还是50节点自己),70没有第3层,往下跳
50来到第2层,找到小于等于70的节点(还是50节点自己),70没有第2层,往下跳
50来到第1层,找到小于等于70的节点(还是50节点自己),70有第1层,50第1层指向70第1层,70第1层指向100第1层
50来到第0层,找到小于等于70的节点(还是50节点自己),70有第0层,50第0层指向70第0层,70第0层指向100第0层
5---------------------->5---------------------------->5->
4---------------------->4---------------->4---------->4->
3---------------->3---->3---------->3---->3---------->3->
2---->2---------->2---->2---------->2---->2---------->2->
1---->1---->1---->1---->1---------->1---->1---->1---->1->
0---->0---->0---->0---->0---->0---->0---->0---->0---->0->
默认 3 10 15 20 30 40 50 70 100
- 查询节点
假设找70节点
肯定不能从第0层开始
从最高层找小于等于70最右的节点(20节点),它不是70,往下跳到第4层
第4层找小于等于70最右的节点(50节点),它不是70
50往下跳到第3层,100 > 70
50往下跳到第2层,还是100
50往下跳到第1层,70,找到了
- 删除节点
删除的时候先查询节点,然后把前面的节点指向删除节点后的节点
时间复杂度
- 利用随机概率生成,0.5的概率为0,0.5的概率为1
- 假如
N个节点- 第0层肯定
N个 - 第1层肯定
N/2个 - 第2层差不多
N/4个
- 第0层肯定
- 相当于一颗完全二叉树
总结
- AVL树,红黑树,SB树相同点和不同点
- 相同点
- 增删改查一样
- 检查时机一样
- 调整的方法一样(左旋,右旋)
- 不同点
- 具体到每个节点的时候,所判断的违规条件不一样
- AVL维持的是高度信息
- SB树维持的是节点个数信息
- 红黑树维持的他自己的标准信息
- 相同点