datetime:2019/5/15 17:46
author:nzb
数据结构和算法
算法:解决问题的方法和步骤
评价算法的好坏:渐近时间复杂度和渐近空间复杂度。
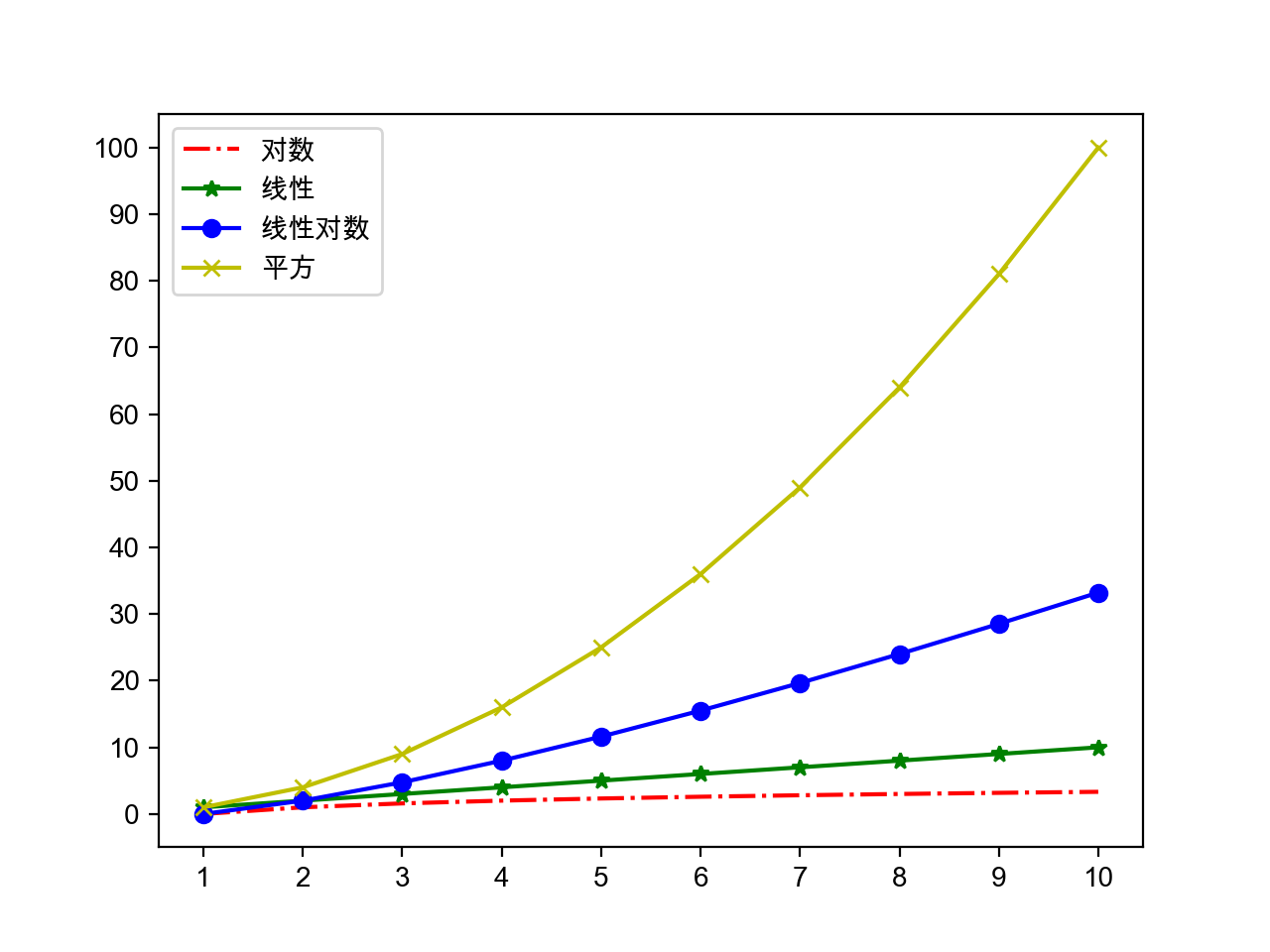
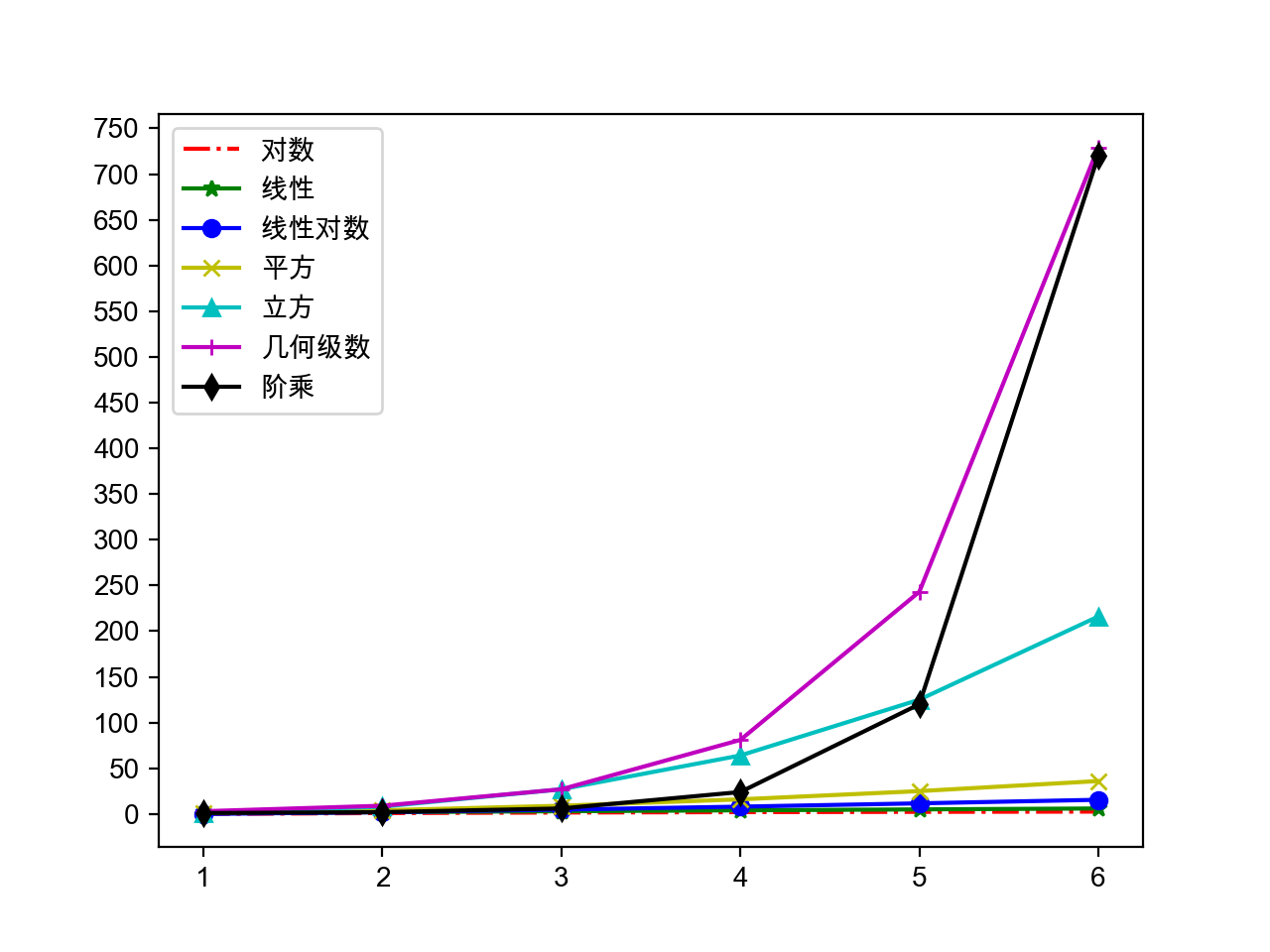
渐近时间复杂度的大O标记:
- 常量时间复杂度 - 布隆过滤器 / 哈希存储
- 对数时间复杂度 - 折半查找(二分查找)
- 线性时间复杂度 - 顺序查找 / 桶排序
- 对数线性时间复杂度 - 高级排序算法(归并排序、快速排序)
- 平方时间复杂度 - 简单排序算法(选择排序、插入排序、冒泡排序)
- 立方时间复杂度 - Floyd算法 / 矩阵乘法运算
- 几何级数时间复杂度 - 汉诺塔
- 阶乘时间复杂度 - 旅行经销商问题 - NP
排序算法(选择、冒泡和归并)和查找算法(顺序和折半)
def select_sort(origin_items, comp=lambda x, y: x < y):
"""简单选择排序"""
items = origin_items[:]
for i in range(len(items) - 1):
min_index = i
for j in range(i + 1, len(items)):
if comp(items[j], items[min_index]):
min_index = j
items[i], items[min_index] = items[min_index], items[i]
return items
# 第一种
def bubble_sort(origin_items, comp=lambda x, y: x > y):
"""高质量冒泡排序(搅拌排序)"""
items = origin_items[:]
for i in range(len(items) - 1):
swapped = False
for j in range(i, len(items) - 1 - i):
if comp(items[j], items[j + 1]):
items[j], items[j + 1] = items[j + 1], items[j]
swapped = True
if swapped:
swapped = False
for j in range(len(items) - 2 - i, i, -1):
if comp(items[j - 1], items[j]):
items[j], items[j - 1] = items[j - 1], items[j]
swapped = True
if not swapped:
break
return items
# 第二种
def bubble_sort(origin_items, comp=lambda x, y: x > y):
"""高质量冒泡排序(搅拌排序)"""
items = origin_items[:]
for i in range(1, len(items)): # 循环次数
for j in range(0, len(items) - i): # 循环索引
if comp(items[j], items[j + 1]):
items[j], items[j + 1] = items[j + 1], items[j]
return items
# 第一种
def merge_sort(items, comp=lambda x, y: x <= y):
"""归并排序(分治法)"""
if len(items) < 2:
return items[:]
mid = len(items) // 2
left = merge_sort(items[:mid], comp)
right = merge_sort(items[mid:], comp)
return merge(left, right, comp)
def merge(items1, items2, comp):
"""合并(将两个有序的列表合并成一个有序的列表)"""
items = []
index, index2 = 0, 0
while index1 < len(items1) and index2 < len(items2):
if comp(items1[index1], items2[index2]):
items.append(items1[index1])
index1 += 1
else:
items.append(items2[index2])
index2 += 1
items += items1[index1:]
items += items2[index2:]
return items
# 第二种
def mergeSort(arr):
if len(arr) < 2:
return arr
middle = len(arr) // 2
left, right = arr[:middle], arr[middle:]
return merge(mergeSort(left), mergeSort(right))
def merge(left, right):
result = []
while left and right:
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
result += left[:]
result += right[:]
return result
def quick_sort(self, li):
# 快速排序 通过
if len(li) < 2:
return li
else:
tmp = li[0]
less = [i for i in li[1:] if i <= tmp]
more = [i for i in li[1:] if i > tmp]
return self.quick_sort(less) + [tmp] + self.quick_sort(more)
def seq_search(items, key):
"""顺序查找"""
for index, item in enumerate(items):
if item == key:
return index
return -1
def bin_search(items, key):
"""折半查找"""
start, end = 0, len(items) - 1
while start <= end:
mid = (start + end) // 2
if key > items[mid]:
start = mid + 1
elif key < items[mid]:
end = mid - 1
else:
return mid
return -1
- 使用生成式(推导式)语法
prices = {
'AAPL': 191.88,
'GOOG': 1186.96,
'IBM': 149.24,
'ORCL': 48.44,
'ACN': 166.89,
'FB': 208.09,
'SYMC': 21.29
}
# 用股票价格大于100元的股票构造一个新的字典
prices2 = {key: value for key, value in prices.items() if value > 100}
print(prices2)
说明:生成式(推导式)可以用来生成列表、集合和字典。
- 嵌套的列表
names = ['关羽', '张飞', '赵云', '马超', '黄忠']
courses = ['语文', '数学', '英语']
# 录入五个学生三门课程的成绩
# 错误 - 参考http://pythontutor.com/visualize.html#mode=edit
# scores = [[None] * len(courses)] * len(names)
scores = [[None] * len(courses) for _ in range(len(names))]
for row, name in enumerate(names):
for col, course in enumerate(courses):
scores[row][col] = float(input(f'请输入{name}的{course}成绩: '))
print(scores)
Python Tutor - VISUALIZE CODE AND GET LIVE HELP
- heapq、itertools等的用法
"""
从列表中找出最大的或最小的N个元素
堆结构(大根堆/小根堆)
"""
import heapq
list1 = [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
list2 = [
{'name': 'IBM', 'shares': 100, 'price': 91.1},
{'name': 'AAPL', 'shares': 50, 'price': 543.22},
{'name': 'FB', 'shares': 200, 'price': 21.09},
{'name': 'HPQ', 'shares': 35, 'price': 31.75},
{'name': 'YHOO', 'shares': 45, 'price': 16.35},
{'name': 'ACME', 'shares': 75, 'price': 115.65}
]
print(heapq.nlargest(3, list1))
print(heapq.nsmallest(3, list1))
print(heapq.nlargest(2, list2, key=lambda x: x['price']))
print(heapq.nlargest(2, list2, key=lambda x: x['shares']))
"""
迭代工具 - 排列 / 组合 / 笛卡尔积
"""
import itertools
itertools.permutations('ABCD')
itertools.combinations('ABCDE', 3)
itertools.product('ABCD', '123')
- collections模块下的工具类
"""
找出序列中出现次数最多的元素
"""
from collections import Counter
words = [
'look', 'into', 'my', 'eyes', 'look', 'into', 'my', 'eyes',
'the', 'eyes', 'the', 'eyes', 'the', 'eyes', 'not', 'around',
'the', 'eyes', "don't", 'look', 'around', 'the', 'eyes',
'look', 'into', 'my', 'eyes', "you're", 'under'
]
counter = Counter(words)
print(counter.most_common(3))
常用算法:
- 穷举法 - 又称为暴力破解法,对所有的可能性进行验证,直到找到正确答案。
- 贪婪法 - 在对问题求解时,总是做出在当前看来是最好的选择,不追求最优解,快速找到满意解。
- 分治法 - 把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题,直到可以直接求解的程度,最后将子问题的解进行合并得到原问题的解。
- 回溯法 - 回溯法又称为试探法,按选优条件向前搜索,当搜索到某一步发现原先选择并不优或达不到目标时,就退回一步重新选择。
- 动态规划 - 基本思想也是将待求解问题分解成若干个子问题,先求解并保存这些子问题的解,避免产生大量的重复运算。
穷举法例子:百钱百鸡和五人分鱼。
# 公鸡5元一只 母鸡3元一只 小鸡1元三只
# 用100元买100只鸡 问公鸡/母鸡/小鸡各多少只
for x in range(20):
for y in range(33):
z = 100 - x - y
if 5 * x + 3 * y + z // 3 == 100 and z % 3 == 0:
print(x, y, z)
# A、B、C、D、E五人在某天夜里合伙捕鱼 最后疲惫不堪各自睡觉
# 第二天A第一个醒来 他将鱼分为5份 扔掉多余的1条 拿走自己的一份
# B第二个醒来 也将鱼分为5份 扔掉多余的1条 拿走自己的一份
# 然后C、D、E依次醒来也按同样的方式分鱼 问他们至少捕了多少条鱼
fish = 1
while True:
total = fish
enough = True
for _ in range(5):
if (total - 1) % 5 == 0:
total = (total - 1) // 5 * 4
else:
enough = False
break
if enough:
print(fish)
break
fish += 1
贪婪法例子:假设小偷有一个背包,最多能装20公斤赃物,他闯入一户人家,发现如下表所示的物品。很显然,他不能把所有物品都装进背包,所以必须确定拿走哪些物品,留下哪些物品。
| 名称 | 价格(美元) | 重量(kg) |
|---|---|---|
| 电脑 | 200 | 20 |
| 收音机 | 20 | 4 |
| 钟 | 175 | 10 |
| 花瓶 | 50 | 2 |
| 书 | 10 | 1 |
| 油画 | 90 | 9 |
"""
贪婪法:在对问题求解时,总是做出在当前看来是最好的选择,不追求最优解,快速找到满意解。
输入:
20 6
电脑 200 20
收音机 20 4
钟 175 10
花瓶 50 2
书 10 1
油画 90 9
"""
class Thing(object):
"""物品"""
def __init__(self, name, price, weight):
self.name = name
self.price = price
self.weight = weight
@property
def value(self):
"""价格重量比"""
return self.price / self.weight
def input_thing():
"""输入物品信息"""
name_str, price_str, weight_str = input().split()
return name_str, int(price_str), int(weight_str)
def main():
"""主函数"""
max_weight, num_of_things = map(int, input().split())
all_things = []
for _ in range(num_of_things):
all_things.append(Thing(*input_thing()))
all_things.sort(key=lambda x: x.value, reverse=True)
total_weight = 0
total_price = 0
for thing in all_things:
if total_weight + thing.weight <= max_weight:
print(f'小偷拿走了{thing.name}')
total_weight += thing.weight
total_price += thing.price
print(f'总价值: {total_price}美元')
if __name__ == '__main__':
main()
分治法例子:快速排序。
"""
快速排序 - 选择枢轴对元素进行划分,左边都比枢轴小右边都比枢轴大
"""
def quick_sort(origin_items, comp=lambda x, y: x <= y):
items = origin_items[:]
_quick_sort(items, 0, len(items) - 1, comp)
return items
def _quick_sort(items, start, end, comp):
if start < end:
pos = _partition(items, start, end, comp)
_quick_sort(items, start, pos - 1, comp)
_quick_sort(items, pos + 1, end, comp)
def _partition(items, start, end, comp):
pivot = items[end]
i = start - 1
for j in range(start, end):
if comp(items[j], pivot):
i += 1
items[i], items[j] = items[j], items[i]
items[i + 1], items[end] = items[end], items[i + 1]
return i + 1
回溯法例子:骑士巡逻。
"""
递归回溯法:叫称为试探法,按选优条件向前搜索,当搜索到某一步,发现原先选择并不优或达不到目标时,就退回一步重新选择,比较经典的问题包括骑士巡逻、八皇后和迷宫寻路等。
"""
import sys
import time
SIZE = 5
total = 0
def print_board(board):
for row in board:
for col in row:
print(str(col).center(4), end='')
print()
def patrol(board, row, col, step=1):
if row >= 0 and row < SIZE and
col >= 0 and col < SIZE and
board[row][col] == 0:
board[row][col] = step
if step == SIZE * SIZE:
global total
total += 1
print(f'第{total}种走法: ')
print_board(board)
patrol(board, row - 2, col - 1, step + 1)
patrol(board, row - 1, col - 2, step + 1)
patrol(board, row + 1, col - 2, step + 1)
patrol(board, row + 2, col - 1, step + 1)
patrol(board, row + 2, col + 1, step + 1)
patrol(board, row + 1, col + 2, step + 1)
patrol(board, row - 1, col + 2, step + 1)
patrol(board, row - 2, col + 1, step + 1)
board[row][col] = 0
def main():
board = [[0] * SIZE for _ in range(SIZE)]
patrol(board, SIZE - 1, SIZE - 1)
if __name__ == '__main__':
main()
动态规划例子1:斐波拉切数列。(不使用动态规划将会是几何级数复杂度)
"""
动态规划 - 适用于有重叠子问题和最优子结构性质的问题
使用动态规划方法所耗时间往往远少于朴素解法(用空间换取时间)
"""
def fib(num, temp={}):
"""用递归计算Fibonacci数"""
if num in (1, 2):
return 1
try:
return temp[num]
except KeyError:
temp[num] = fib(num - 1) + fib(num - 2)
return temp[num]
动态规划例子2:子列表元素之和的最大值。(使用动态规划可以避免二重循环)
说明:子列表指的是列表中索引(下标)连续的元素构成的列表;列表中的元素是int类型,可能包含正整数、0、负整数;程序输入列表中的元素,输出子列表元素求和的最大值,例如:
输入:1 -2 3 5 -3 2
输出:8
输入:0 -2 3 5 -1 2
输出:9
输入:-9 -2 -3 -5 -3
输出:-2
def main():
items = list(map(int, input().split()))
size = len(items)
overall, partial = {}, {}
overall[size - 1] = partial[size - 1] = items[size - 1]
for i in range(size - 2, -1, -1):
partial[i] = max(items[i], partial[i + 1] + items[i])
overall[i] = max(partial[i], overall[i + 1])
print(overall[0])
if __name__ == '__main__':
main()