datetime:2024/2/24 16:49
author:nzb
字符串匹配算法
KMP算法
字符串str1和str2,str1是否包含str2,如果包含返回str2在str1中开始的位置。如何做到时间复杂度O(N)完成?
- 问题引入:首先我们来看一个例子,现在有两个字符串A和B,问你在str1中是否有str2,为了方便叙述,我们先给定两个字符串的值
- A="abcaabababaa"
- B="abab"
暴力解法
- 首先我们能想到规定头指针,并依次向后比较的暴力方法
- 从主串s的第一个字符开始,与模式串m的第一个字符比较,若相等,则继续逐个比较后序字符;
- 否则从主串下一个字符起,重新和模式串的第一个字符开始比较
- 在暴力匹配中,每趟匹配失败都是模式后移一位再从头开始比较,这种频繁的重复比较相当于模式串在不断地进行自我比较,这是低效的根源。
KMP算法
在讲KMP算法之前我们需要先介绍最长前缀和后缀匹配长度
- 1、前缀和后缀最长匹配长度
- 前缀:指除了最后一个字符以外,字符串所有头部子串(以头部字符开始)
- 后缀:指除了第一个字符(当前字符)以外,字符串所有尾部子串(以尾部字符结束)
- 下面以字符abbabbk为例进行说明
k字符为例:- 长度为1时:前缀:
a, 后缀:b, 最长匹配长度为0 - 长度为2时:前缀:
ab, 后缀:bb, 最长匹配长度为0 - 长度为3时:前缀:
abb, 后缀:abb, 最长匹配长度为3 - 长度为4时:前缀:
abba, 后缀:babb, 最长匹配长度为0 - 长度为5时:前缀:
abbab, 后缀:bbabb, 最长匹配长度为0 - 长度为6时:就是整个子串,不考虑
- 所以
k字符的最长前缀和后缀匹配长度为3
- 长度为1时:前缀:
2、next数组
- 基于前缀和后缀最长匹配长度的计算,我们需要算出m字符串每一个字符之前对应的信息,将这些信息用数组
next[]存储起来 以aabaabs为例:next[]={-1, 0, 1, 0, 1, 2, 3} - 元素还有另外一层作用就是要调到元素的索引,比如长度为3,索引是0~2,下一个元素索引就是3
- 人为规定,第一个元素长度为-1,第二个元素长度为0
- 基于前缀和后缀最长匹配长度的计算,我们需要算出m字符串每一个字符之前对应的信息,将这些信息用数组
3、KMP算法 图解:
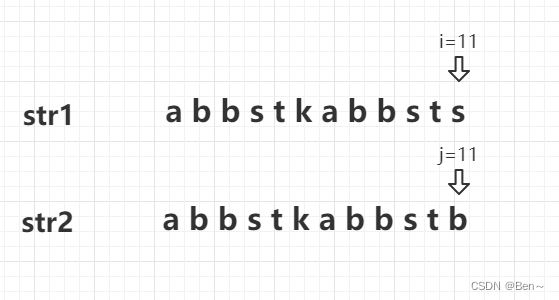
当str1和str2匹配到第11位时出现了不相等的情况,此时str1的i指针不动,str2的j指针指向该字符对应最长匹配长度的下一位即j=5
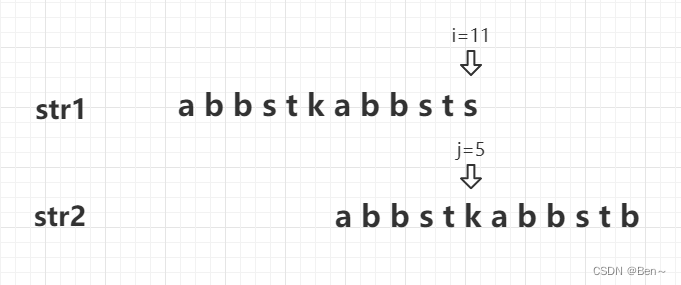
再将此时i和j指向的字符进行比较
我们可以将该过程理解为将str2往右移i-j位,str2在j之前的字符已经匹配,不用再进行比较。
该过程的实质是:
- 1、将
str2推到j位置开头,并从可能不相等的位置往下走 2、
str1从0开始到j之前不存在任何一个位置能配出str2,注意是整个str2为啥不存在呢,跟
next数组含义有关,利用反证法证明str1 = i ............... k ........... | j........... x str2 = 0 ..匹配长度....|................| ....匹配长度.. y 假设 j~x 是最长前缀和后缀匹配长度 假设中间任意一个位置k,能配出整个str2,注意是整个 那么从k出发到x之前这一段,必须跟str2等量的区域(或前缀)一样才行,为什么,因为从str1和str2一路相等,到x和y位置才不等的 那就说明k~x之前的字符串等于str2的等量的前缀,那就找到了一个更长的匹配长度,跟next数据冲突了
只要理解了这两个实质,该算法就基本上理解了。
- 示例
index 0123456 78 9 10 11 12 13 14 15 16
str1 = abbsabb tc a b b s a b b e
str2 = abbsabb tc a b b s a b b w
- 比对到16,e != w
- 继续,此时str2 最长前缀为7,str2 回退到位置 7,str1位置还是16,相当于从str1的位置9和str2开始比对,此时,e != t
- 继续,此时str2 最长前缀为3,str2 回退到位置 3,str1位置还是16,相当于从str1的位置13和str2开始比对,此时,e != s
- 继续,此时str2 最长前缀为0,str2 回退到位置 0,str1位置还是16,相当于从str1的位置16和str2开始比对,此时,e != a
- 此时不能往前退了,str1位置加1,从17位置开始和str2开头开始比对
代码
def kmp(str1, str2):
if not str1 or not str2 or len(str1) < len(str2):
return -1
idx1 = 0
idx2 = 0
next_arr = get_next_array(str2)
while idx1 < len(str1) and idx2 < len(str2):
if str1[idx1] == str2[idx2]:
idx1 += 1
idx2 += 1
elif next_arr[idx2] == -1: # == idx==0 表示str2已经来到头位置,不能再往前跳了
idx1 += 1
else:
idx2 = next_arr[idx2]
# i1越界或i2越界
return idx1 - idx2 if idx2 == len(str2) else -1
def get_next_array(str_data):
"""
求第i位的最长匹配长度,获取到i-1的最长匹配长度,然后拿i-1位置字符和next[i-1]位置作比较,如果相等,则i的最长长度是i-1的最长长度+1
如果不一样,再从next[i-1]往前跳最长匹配长度
0 3 8 i-1 i
str = abbstabb ec abbstabb ?
i-1 位置长度为8(e字符)
看e跟?是否相等
相等 8+1,
不等再往前跳,e字符长度3(s字符)
看s跟?是否相等
相等 3+1,
不等再往前跳,s字符长度0(a字符)
看a跟?是否相等
相等 1,
不等往前跳不了了,则为0
:param str_data:
:return:
"""
if len(str_data) == 1:
return [-1]
next_arr = [-1, 0]
idx = 2 # next数组的位置
cn = 0 # 需要和i-1作比较的位置
while idx < len(str_data):
if str_data[idx - 1] == str_data[cn]:
cn += 1
next_arr[idx] = cn
idx += 1 # 计算下一个字符的最长匹配长度
# 和 i-1位置匹配不上,当前跳到cn位置
elif cn > 0:
cn = next_arr[cn]
else:
next_arr[idx] = 0
return next_arr
时间复杂度
- 暴力解法的时间复杂度为:
O(m*n),其中m为str2的长度,n为str1的长度 KMP算法的时间复杂度为:O(m+n),其中m为计算next数组的时间复杂度,n为KMP进行匹配时的时间复杂度
Manacher 算法
又称“马拉车算法”,主要用于求解最长回文子串的长度
经典最长回文子串长度求法
从字符串的每个字符开始,向左右两边扩,算出以每个字符为中心的回文子串的长度,然后取最大值。
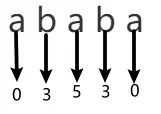
但是用这种方法只能算出奇回文子串的长度,无法算出偶回文子串的长度,如下图所示,这是一个长度为 4 的回文串,但用上面的方法没办法算出它的长度,因为上面的方法是以一个字符为中心算长度,但是偶回文子串的中心并不是一个字符。
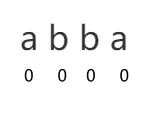
为了可以计算出偶回文子串的长度,我们可以对字符串做一些变化,把 “abba” 变成 “#a#b#b#a#” ,然后按照上面的方面再计算一次,就可以算出来了,最大值除以 2 向下取整就是最长回文串的长度。
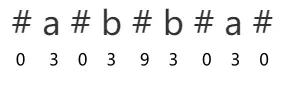
这里是在原字符串的每个字符前后加了特殊符号 “#”,但其实这个特殊符号加什么都行,只是为了方便,就算原字符串中本来就有 “#” 也不会有影响,因为我们可以发现在比较的时候原字符只会与原字符进行比较,特殊字符只与特殊字符比较。
整个过程的时间复杂度为 O(N^2),例子#1#1#1#1#1#1#1#1#,遍历走一遍,然后比较走到某一端
Manacher 算法
与 KMP 有点类似,就是对经典的算法做一个加速
几个重要的概念
以字符串#a#b#b#a#b#b#a#为例
回文半径:从中心字符到回文子串结束的距离,如回文子串 #a# 的回文半径就是 2,#a#b#b#a# 的回文半径是5
回文半径数组 pArr:与 KMP 的 next 数组有点类似,回文半径数组存放的是每个字符对应回文子串的半径
最右回文右边界 R:之前所有的回文子串的最右的边界
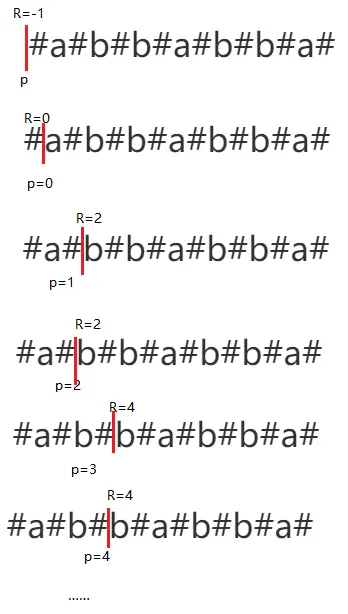
最右回文右边界的中心 C:即最右回文有边界对应的回文串的中心位置
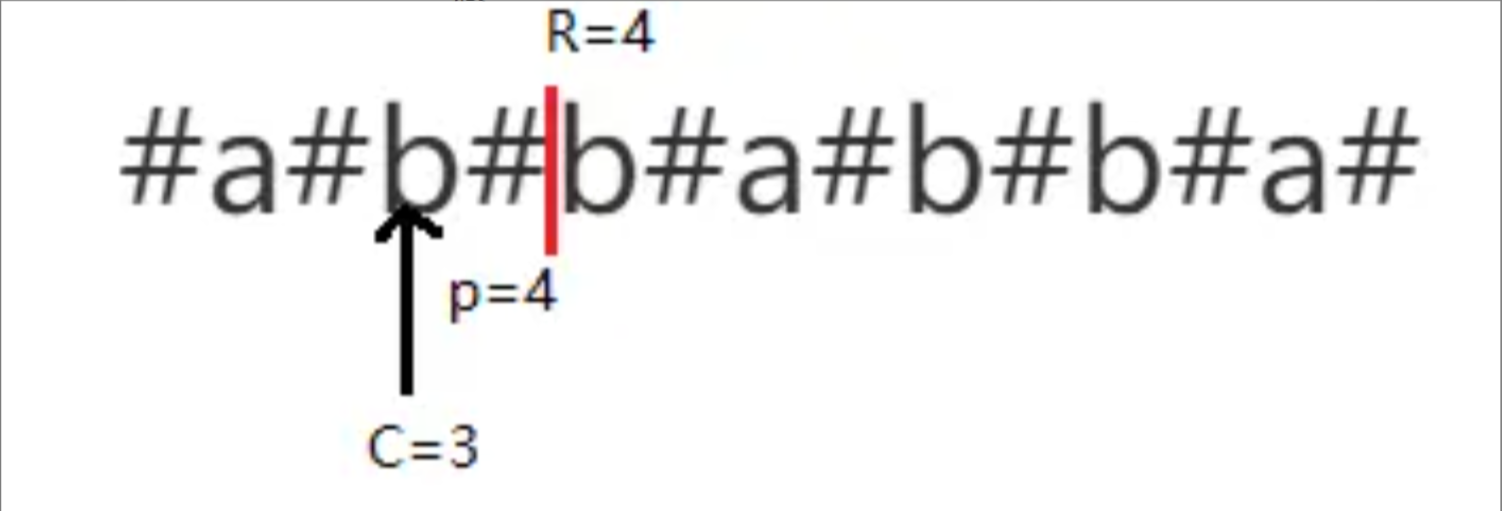
Manacher算法流程
主要是计算回文半径数组 pArr,分为两种情况
1)下一个字符的位置
i不在R里,这种情况R直接暴力往右扩,且以这个字符为中心的回文子串的长度至少为12)下一个字符的位置
i在R里,找到i相对于C的对称点j,这时又分为三种情况,记R相对于C的字符为L,[L...j...C...i...R]即为以C为中心最长回文子串- ①
j为中心的整个回文子串(下面称j回文子串)在[L......R]里,那么i为中心的回文子串(下面称i回文子串)半径与以j回文子串半径相等 - ②
j回文子串部分在[L......R]里,那么i回文子串半径为R - i - ③
j回文子串的左边界正好等于L,那么i回文子串半径至少为R - i,然后继续往外扩
- ①
证明,主要证
2)部分,前面2中不用试就知道答案,第3种情况需要去试才知道会不会更长①如示例:
[L..x(..j..)y..C..p(..i..)q..R],j左右的小括号区域(下面称为j区域)代表j回文子串 ,因为L到R是以C为中心的最长回文子串,所以i左右的小括号区域 (下面称为i区域)与j区域一定是互相逆序的,又因为j区域是回文子串,所以i区域也是回文子串。那么如何确定它是最大呢? 我们假设x是以j回文子串前一个字符,y是后一个字符,p、q同理分别为以i回文子串前一个和后一个字符,我们假设刚才的回文子串不是最大, 那么p和q必是相等的,按照回文串的性质,p和y相等(因为L~R关于C对称),q和x相等,则x和y一定是相等的,但是j回文子串是不包括x和y的, 也就是说x和y不可能相等,即p和q不可能相等,假设不成立,所以i回文子串半径一定与j回文子串半径相等。
②
j回文子串不全在[L...R]里,部分超出,如示例:..(x[L..j..L'y)..C..pR'..i..R]q..,找到L相对于j的对称点L',由回文串的性质可知,[L..j..L']一定是回文子串, 所以与之对应[R'..i..R]也是回文串,所以i回文子串的半径最小是R - i。那有没有可能更大呢?不可能。x是L的前一个字符,y是L'的后一个字符,p是R'的前一个字符,q是R后一个字符。i回文子串半径要想更大,就需要p和q相等, 我们现在已知x和y都属于j回文子串,所以x和y相等,y和p相等,即x和p相等,因为以C为中心的最长回文子串的左右边界是L和R, 所以x和q是不可能相等的,结合起来就是p不可能等于q,所以i的回文子串半径最大为R - i。
③
j回文子串的左边界正好等于L,如示例:[(L..j...)..C.p(...i..R)]q,首先我们可以肯定i回文子串至少是R - i,至于能不能继续扩大,就需要看p能不能等于q, 从图中可以看出,与前面两种情况不同,p等不等于q,并不会破坏j回文子串和以C为中心的回文子串,所以p是可以等于q的,如果p等于q, 那么R往右扩,i回文子串半径+1,直到不能继续向右为止。
时间复杂度O(n)
具体分析过程,可以看左神的视频讲解
def manacher(str_data):
if not str_data:
return 0
# 用特殊字符拼接
str_new = "#" + "#".join(list(str_data)) + "#"
p_arr = [1] * len(str_new) # 回文半径数组
c = -1 # 中心
r = -1 # 回文右边界的再往右一个位置 最右的有效区是R-1位置
max_val = float("-inf") # 扩出来的最大值
for i in range(len(str_new)): # 每个位置都求回文半径
# p_arr[i] 表示至少的回文区域,就是我们不用验证就知道有多少的区域
# 2 * c - i 就是 j 的位置,也就是i关于 c 对称的位置,则 p_arr[2*c-i]就是j和i的回文半径
"""
* 同时满足上面的两类情况
* 1)如果 R < i,即 i 不在 R 里,那么半径至少为 1(不用验证)
* 2)如果 R > i,即 i 在 R 里,那么
* 为什么取两者的较小值呢?
* 首先三种情况:
* 如果 j 回文子串完全在 C 回文子串里,那么 i 回文子串半径就是 p_arr[2 * C - i],因为包含所以 R - i >= p_arr[2 * C - i],即至少不用验证 min(p_arr[j], R - i),选 p_arr[2 * C - i]
* 如果 j 回文子串在部分在 C 回文子串里,那么 i 回文子串半径就是 R - i,因为C的回文到R,所以 R - i <= p_arr[2 * C - i],即至少不用验证 min(p_arr[j], R - i),选 R-i
* 如果 j 回文子串左边界正好等于 C 回文子串的左边界,那么 i 回文子串半径至少为 R - i,跟第二种情况一样,所以至少不用验证 min(p_arr[j], R - i),选 R-i
* 所以直接写成了 min(p_arr[2 * c - i], r - i)
"""
p_arr[i] = min(p_arr[2 * c - i], r - i) if r > i else 1
"""
主要针对 R < i 和 j 回文子串左边界正好等于 C 回文子串的左边界这两种情况,回文子串需要扩充
idx = 0123456
str = #a#b#a#
arr = 1214121
arr[i]存放了当前位置的最少的回文半径,char[i + arr[i]]char[i - arr[i]分别是当前字符的回文子串的后一个和前一个字符,相等则 arr[i]++,否则break
虽然上面 j 回文子串完全在 C 回文子串里和 j 回文子串在部分在 C 回文子串里时,arr[i] 已经是确定值,不需要再扩充,
但为了代码方便,减少 if else 使用,直接全部扩充,不需要的扩充的仅需进行一次判断就 break了,对代码整体时间复杂度影响不大
"""
while i + p_arr[i] < len(str_new) and i - p_arr[i] > -1:
if str_new[i + p_arr[i]] == str_new[i - p_arr[i]]:
p_arr[i] += 1
else:
break
if (i + p_arr[i]) > r:
r = i + p_arr[i]
c = i
max_val = max(max_val, p_arr[i])
# max 中包括是 # 字符的半径,max - 1正好是原回文串的长度
# #1#2#1#,回文半径2#1#,长度是4,除去拼接的#实际是121,长度为3
# #a#b#b#a#,回文半径#b#a#,长度5,除去拼接的#实际是abba,长度为4
return max_val - 1
print(manacher("121"))
print(manacher("abba"))