datetime:2024/6/16 16:07

author:nzb

Kalman Filtering(卡尔曼滤波)

入门

^表示估计值

-表示先验估计值

• 引入

• 适用系统：线性高斯系统

  • 线性：满足叠加性和齐次性

    

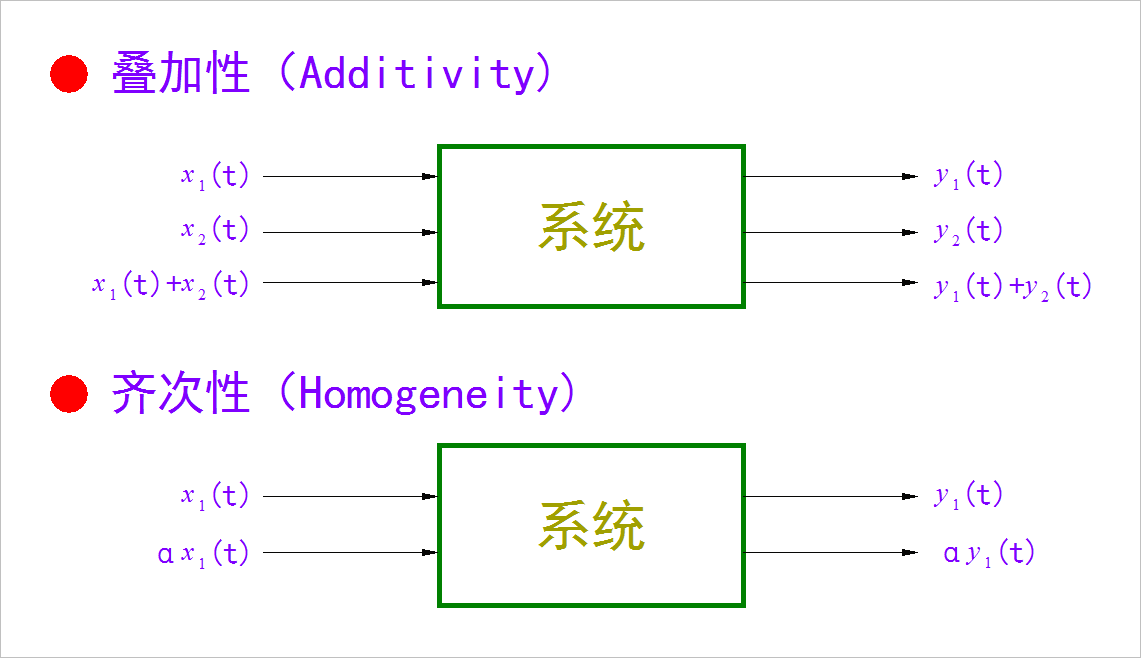
  • 高斯：噪声满足高斯分布(正态分布)

    • μ：均值
    • σ：方差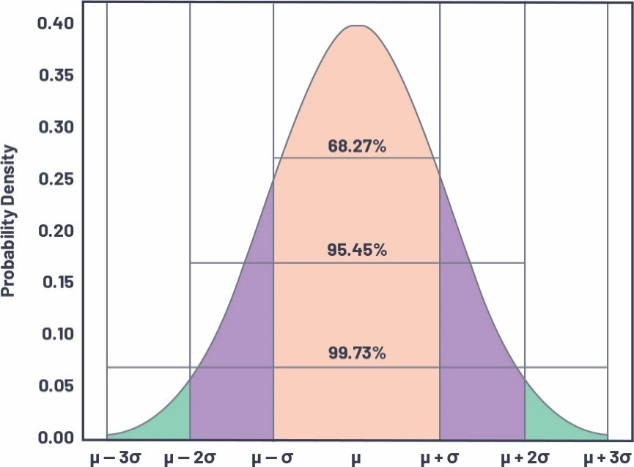

• 宏观意义：滤波即加权

  • 理想状态：信号 1 + 噪声 0
  • 低通滤波：低频信号 1 + 高频信号 0
    • 因为大多情况下高频信号一般为噪声
  • 卡尔曼滤波：估计值 (权重) + 观测值 (权重)

进阶

• 状态空间表达式(跟卡尔曼滤波方程相似)

  • 状态方程

    $x_{k} = A_{x_{k-1} } + Bu_{k} + W_{k}$

    • $x_{k}$：当前状态的当前值
    • $A$：状态转移矩阵，即当前状态上一刻的值乘上某种关系作用到 $x_{k}$
    • $x_{k-1}$： 上一时刻该状态的值
    • $B$： 控制矩阵，即输入乘上某种关系作用到 $x_{k}$
    • $u_{k}$： 输入，给到 $x_{k}$ 的输入
    • $W_{k}$： 过程噪声

  • 观测方程

    $y_{k} = Cx_{k} + V_{k}$

    • $y_{k}$： 要观察的量
    • $C$： $x_{k}$ 乘上某种关系得到你要观察的值
    • $x_{k}$： 状态量
    • $V_{k}$： 观测噪声

  • 示例

    

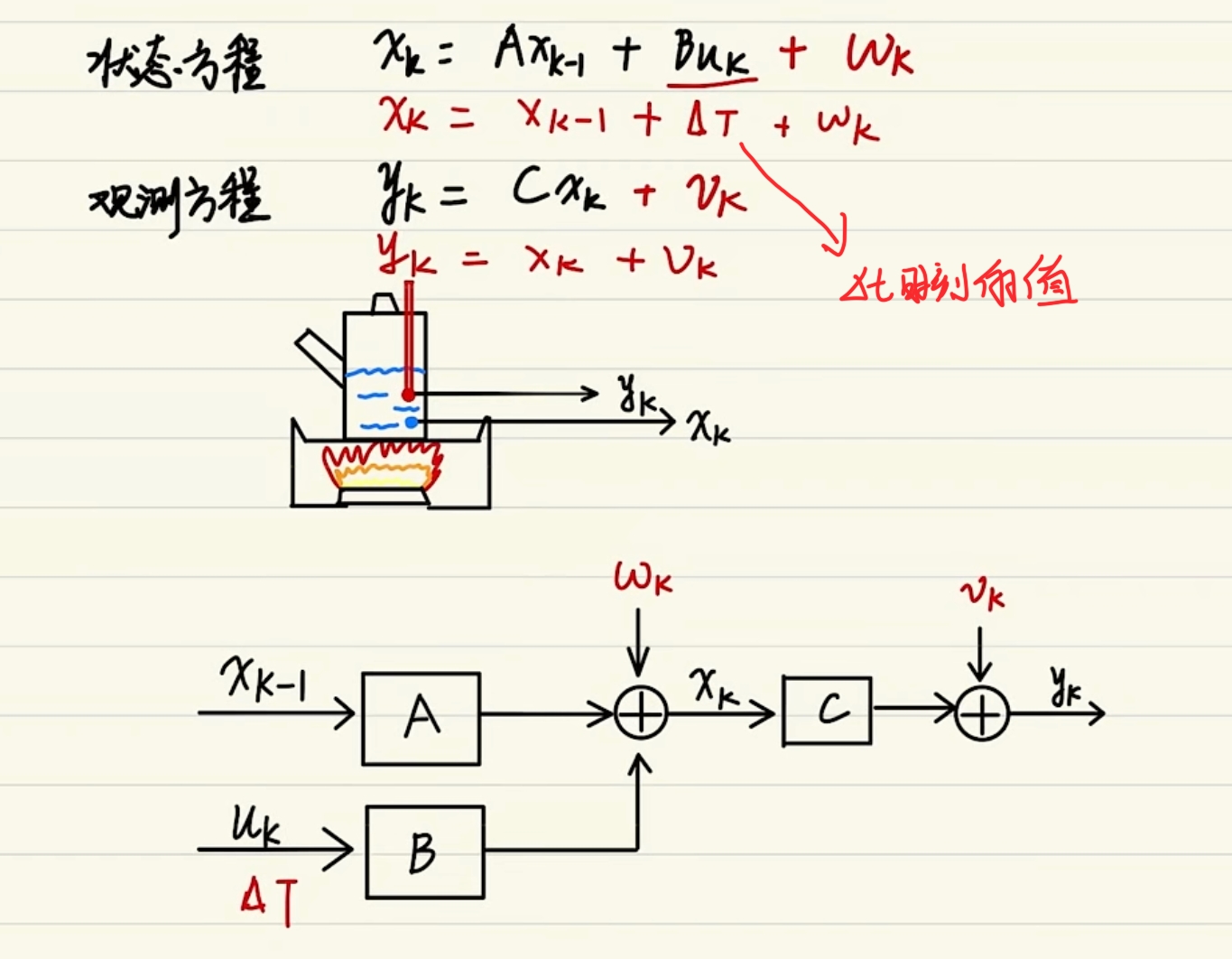
    举个例子看一下，这个是火炉对水加温， 那么这个蓝色的点呢就是水温的状态，这个红色是温度计，那么温度计是一个传感器， 输出是一个yk，就是水温的值，那么很明显，这个时候这个C就是1。 然后这边有一个误差，温度计也有误差，所以它输出的是观测方程下红色的那个方程， 然后这边水温假设它是一个线性变化的，那么这个时候b乘uk就相当于得塔，每一时刻会增加多少度的温度， 然后我们在这边的过程噪声也可以考虑进去，因为除了火炉对水加热之外， 还有外面的环境，会影响它，所以它的过程温度并不是那么理想，然后这个要加一个过程噪声， 然后这边是一个当前的水的温度值，温度值的话是基于之前的水温的，那么这个时候A只要取一个单位矩阵就好了。 所以这个为状态方程下红色的方程，那么用一个方框图来表示如上图所示。

• 高斯分布

  • 直观图解

    

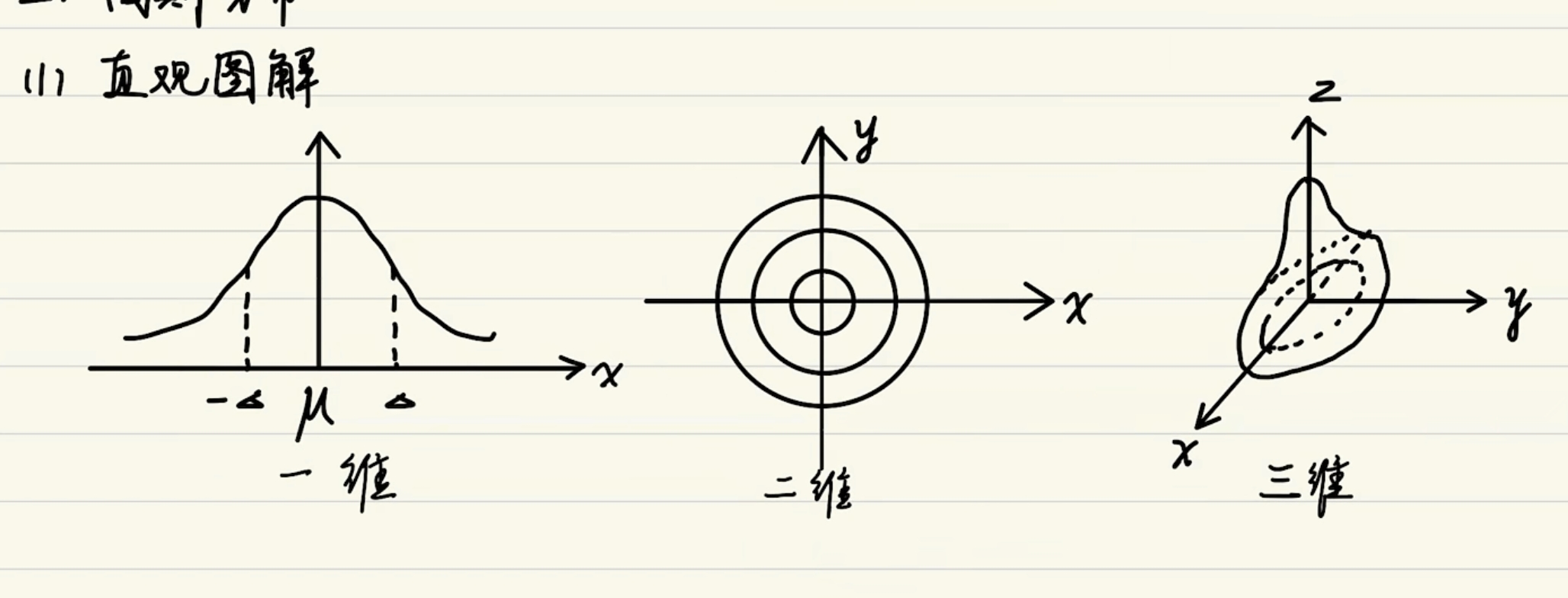
  • 参数分析

    • 高斯白噪声：$W_{k}$ 和 $V_{k}$
      • $W_{k} \in N(0;Q_{k})$；过程噪声，符合正态分布，均值为0，方差为 $Q_{k}$
      • $V_{k} \in N(0;R_{k})$：观测噪声，符合正态分布，均值为0，方差为 $R_{k}$
      • 示例：解释 $V_{k}$ 和 $R_{k}$ 定义
        • GPS检测到一辆车的position，开了1000m，但是GPS还是有精度误差的，所以为1000 ± δ m
        • δ就为噪声(误差)，则 $V_{k} = \delta m$
        • δ符合正态分布，方差为 1m噪声(假设)，所以 $R_{k} = 1 m$
      • 示例：解释 $W_{k}$ 和 $Q_{k}$ 定义
        • 假设有一个滑板，假设速度为 5m/s，由于风的作用，所以变成了 5m/s ± δ m/s
        • δ就为噪声(误差)，则 $W_{k} = \delta m/s$
        • 假设δ符合正态分布，方差为 1m/s噪声(假设)，所以 $\delta \in (0,1),所以 Q_{k} = 1m/s$

    • 方差

      • 一维方差
        • 过程和观测方差：$Q_{k}$ 和 $R_{k}$
        • 状态(估计值)方差：$\hat{\phantom{\;;}x_{t}^{-}}$，一个值，该状态也符合正态分布
      • 二维协方差$cov(x,y)$
        • $\hat{\phantom{\;;}x_{t}^{-}} = \begin{bmatrix}\hat{\phantom{\;;}x_{t1}^{-}} \\ \hat{\phantom{\;;}x_{t2}^{-}}\end{bmatrix}\begin{matrix}\to W_{k1}\\\to W_{k2}\end{matrix}$
        • $cov(\hat{\phantom{\;}x_{t1}^{-}}, \hat{\phantom{\;}x_{t2}^{-}}) = \begin{bmatrix} cov(x_{1}, x_{1})& cov(x_{1}, x_{2})\\ cov(x_{2}, x_{1})& cov(x_{2}, x_{2}) \end{bmatrix}$
      • 多维协方差矩阵C
        • $C = \begin{bmatrix}cov(x_{1}, x_{1}) & cov(x_{1}, x_{2}) & ... & cov(x_{1}, x_{n})\\cov(x_{2}, x_{1}) & cov(x_{2}, x_{2}) & ... & cov(x_{2}, x_{n})\\\vdots & \vdots & \ddots & \vdots\\cov(x_{n}, x_{1}) & cov(x_{n}, x_{2}) & ... & cov(x_{n}, x_{n})\\\end{bmatrix}$

• 超参数：Q、R，相当于调PID

  • Q：过程噪声方差
  • R：观测噪声方差
  • 主要就是调这两个参数

• 卡尔曼直观图解

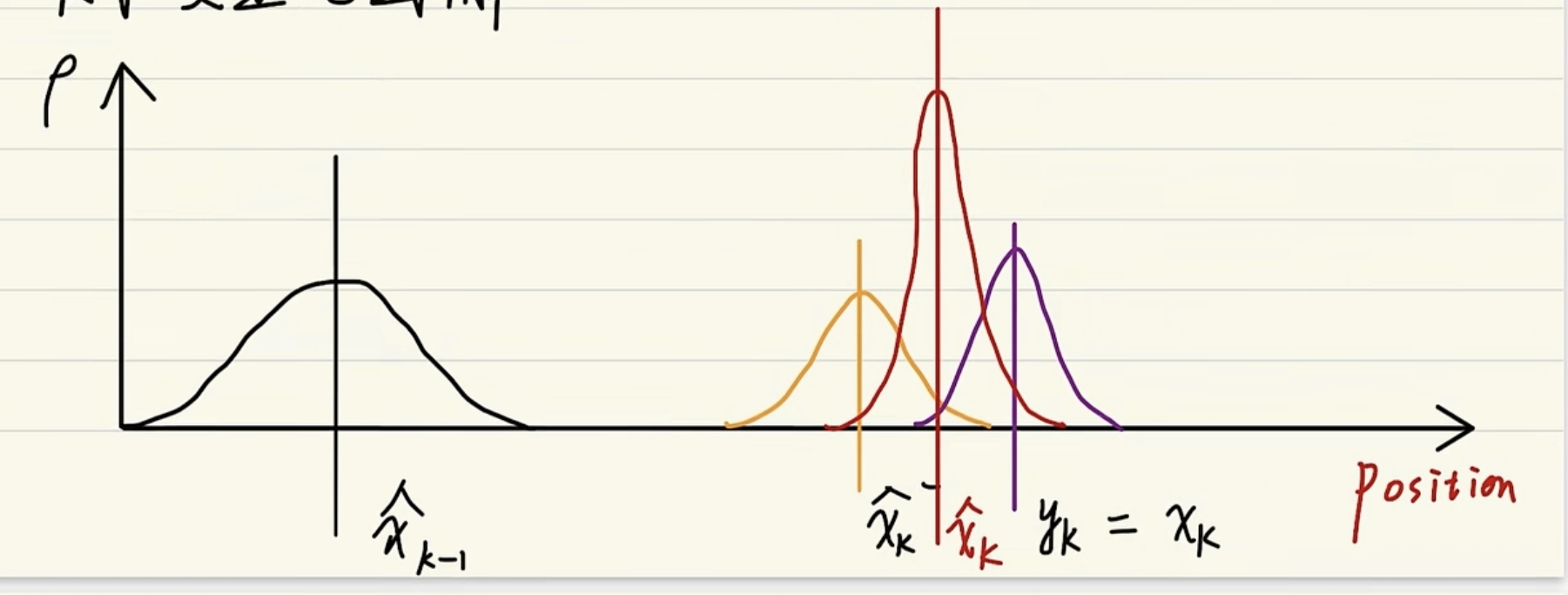
• x轴为位置，y轴为概率密度
• $\hat{\phantom{\;;;}x_{k-1}}$ ：无横杆，表示最优估计值，也叫修正值，后验估计值，卡尔曼滤波输出的值
• $\hat{\phantom{\;;;;}x_{k}^{-}}$ ：先验估值值，基于最优估计值得出的
• $y_{k}$ ：观测值，相当于直接等于x_{k}，传感器直接测量出来的值
• $\hat{\phantom{\;;;;}x_{k}}$ ：当前时刻的最优估计值，明显方差更小，因为滤波次数过多，方差变小，趋于稳定
  • 当前的最优估计值是由：先验估计值 和 当前的观测值取公有的部分得到一个最优的值

放弃

卡尔曼公式理解

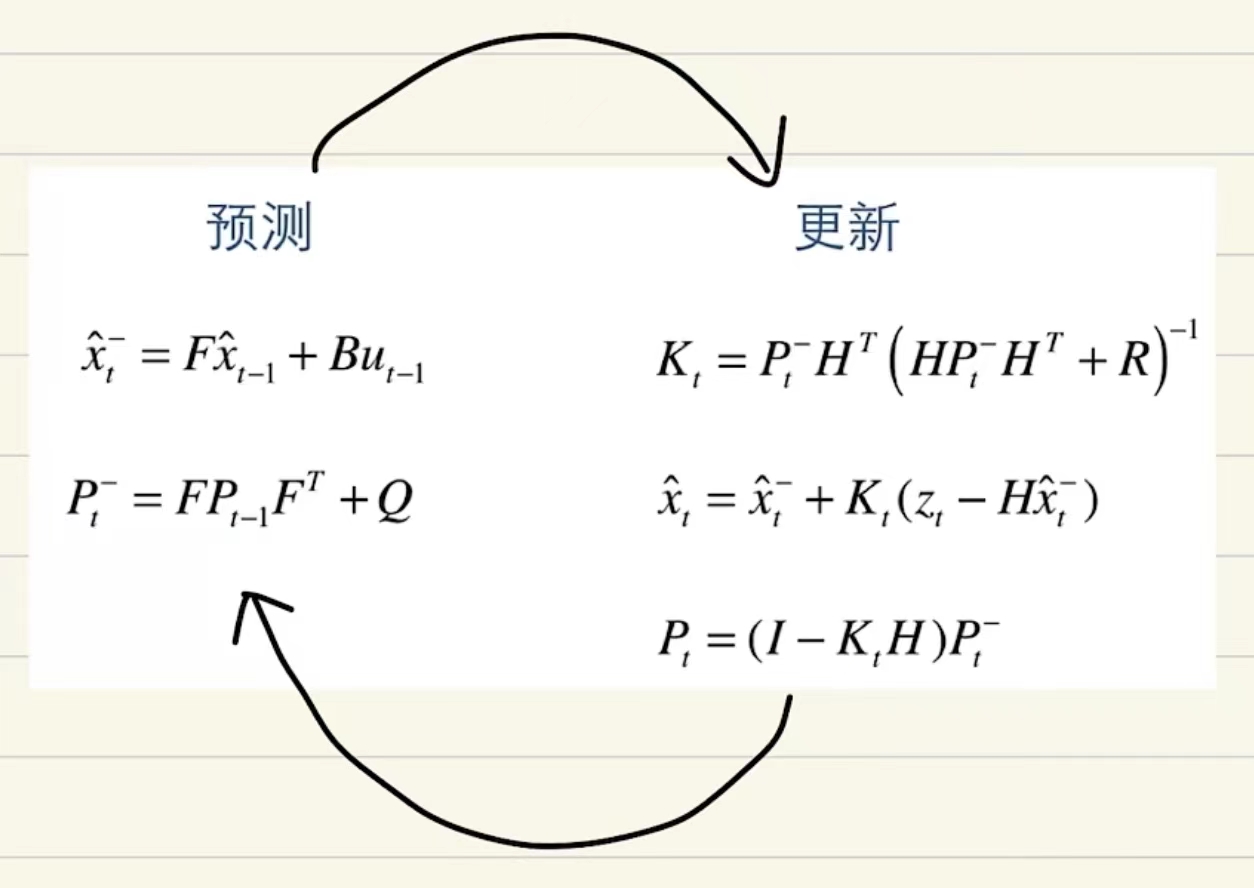
实现过程：使用上一次的最优结果(先验估计)预测当前的值，同时使用观测值(传感器的值)修正当前值，得到最优结果

• 预测
  • $\hat{\phantom{\;;}x_{t}^{-}} = \hat{\phantom{\;;}{F}x_{t-1}} + Bu_{t-1}$
    • 基于之前的最优估计推出当前阶段的先验估计
  • $P_{t}^{-} = FP_{t-1} + Q$
    • 协方差公式，对应上面的 $\hat{\phantom{\;;}x_{t}^{-}}$ 的协方差矩阵

• 更新

  • $K_{t} = P_{t}^{-}H^{T}(HP_{t}^{-}H^{T} + R)^{-1}，卡尔曼增益$
  • $\hat{\phantom{\;}x_{t}} = \hat{\phantom{\;;}x_{t}^{-}} + K_{t}(z_{t} - H\hat{\phantom{\;}x_{t}^{-}} )$
    • 最优估计(估计值+观测值)，先验估计 $\hat{\phantom{\;;}x_{t}^{-}}$ 加上卡尔曼增益乘上观测值减去先验估计值，$K_{t}(z_{t} - H\hat{\phantom{\;}x_{t}^{-}} )$ 为观测值
  • $P_{t} = (I - K_{t}H)P_{t}^{-}$
    • 后验估计协方差矩阵更新，基于原来预测估计的协方差矩阵乘以一个因子得出

• 示例

  

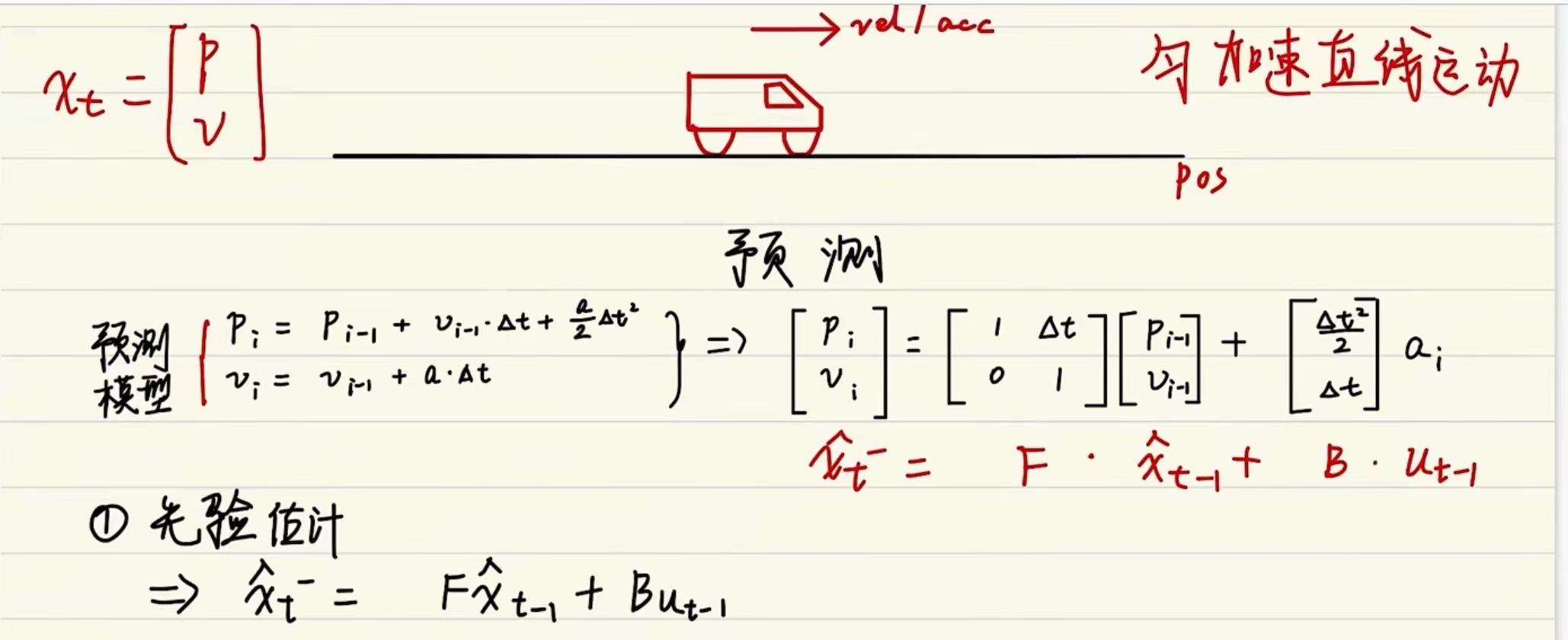
  • 先验估计
    $\hat{x_{t}^{-}} = F\hat x_{t-1} + Bu_{t-1}$

  • $预测模型\left.\begin{matrix}p_{i} = p_{i-1} + v_{i-1}\cdot \Delta t + \frac{a}{2} \Delta t^{2} & \\v_{i} = v_{i-1} + a \cdot \Delta t &\end{matrix}\right\}\Rightarrow \begin{bmatrix} p_{i}\\ v_{i}\end{bmatrix} = \begin{bmatrix} 1 & \Delta t \\ 0 & 1\end{bmatrix}\begin{bmatrix} p_{i-1}\\ v_{i-1}\end{bmatrix}+\begin{bmatrix}\frac{\Delta t^{2}}{2} \\\Delta t\end{bmatrix}a_{i}$

  • 先验估计协方差： $P_{t}^{-} = FP_{t-1}F^{T} + Q$

    • 是由上面先验估计得出的，Q是上面先验估计的过程噪声 $W_{t}$
      • 通常：cov(x, x) = Var(x)
      • 通常：cov(Ax, Ax) = Acov(x,x)A^T
      • 通常：cov(Ax+k, Ax+k) = Acov(x,x)A^T，k为常数
      • $cov(\hat x_{t}^{-}, \hat x_{t}^{-}) \\先验估计代入\Rightarrow cov(F\hat x_{t-1}+Bu_{t-1} + W_{t},F\hat x_{t-1}^{-}+Bu_{t-1} + W_{t})\\ \Rightarrow Fcov(\hat x_{t-1}, \hat x_{t-1})F^{T} + cov(W_{t}, W_{t})$
        • $cov(\hat x_{t-1}, \hat x_{t-1})，就是P_{t-1}$
        • $cov(W_{t}, W_{t})，就是Q$
        • 化简就是最初的先验估计协方差公式

  • 测量方程：Z_v取0是为了凑维度，H和后面那个矩阵可以写成[[1,0][0,0]]

  • 状态更新

    • $更新卡尔曼增益：K_{t} =\frac{P_{t}^{-}H^{T}}{HP_{t}^{-}H^{T} + R} \\\Rightarrow (假设一维，H简化为1) \frac{P_{t}^{-}}{P_{t}^{-} + R}\\\Rightarrow \frac{P_{t-1} + Q}{P_{t-1} + Q + R} 所以卡尔曼增益是跟Q和R有关的，R观测噪声方差$

  • 

调节超参数

• Q与R的取值

  

  • 公式层面理解
    • 当需要更信任观测值(观测值也有噪声)的时候，K就需要增大，R越小，K越大，越相信观测值
    • 当运动模型很完美，更相信估计值，需要K小，则Q小一点，R大一点
  • 其他层面理解
    • Q：过程噪声，如果运动模型非常完美，比如小车在光滑地面，没有风阻，这个时候运动模型基本没有噪声，则Q可以小一点，否则大一点
    • R：观测噪声，根据传感器觉得，如果精度不高噪声大，R需要大一点

• $P_{0}$ 和 $\hat x_{0}$ 的取值

• • 比较随意，经过迭代后期会趋于稳定值
  • 习惯取 $\hat x_{0} = 0$，P0往小的取，方便收敛（一般取1，不可为0）

卡尔曼滤波的使用

• 选择状态量，观测量
• 构建方程
• 初始化参数：Q,R,P0,x0
• 代入公式迭代
• 调节超参数：Q,R，需要多次人工调节

精通

卡尔曼滤波公式回顾

• 离散控制系统不需要滤波

机器人应用举例

陀螺仪滤波

• 选择状态量，观测量
  • $状态量\begin{bmatrix} angle (角度)\\Q\_bias (陀螺仪漂移)\end{bmatrix}\\观测量\begin{bmatrix} new\_angle (输出角度)\\\end{bmatrix}$
  • 明确一下参数
    • 陀螺仪噪声协方差：Q_angle，对应状态量的angle
    • 陀螺仪漂移噪声协方差：Q_gyro，对应状态量的Q_bias
    • 角度测量噪声协方差：R_angle，对应观测量的new_angle
    • 陀螺仪测得的角速度：newGyro
    • 采样周期：dt
• 构建方程
  • 预测当前角度
    • $由先验估计非常 X(k|k-1) = AX(k-1|k-1) +Bu(k) + W(k) \\之前上面的公式 \begin{bmatrix} p_{i}\\ v_{i}\end{bmatrix} = \begin{bmatrix} 1 & \Delta t \\ 0 & 1\end{bmatrix}\begin{bmatrix} p_{i-1}\\ v_{i-1}\end{bmatrix}+\begin{bmatrix}\frac{\Delta t^{2}}{2} \\\Delta t\end{bmatrix}a_{i}$
    • $预测模型\left.\begin{matrix}angle_{i} = angle_{i-1} - Q\_bias \cdot dt + newGyro \cdot dt\\Q\_bias = Q\_bias\end{matrix}\right\} \\构建方程\Rightarrow \begin{bmatrix} angle\\ Q\_bias\end{bmatrix} = \begin{bmatrix} 1 & -dt \\ 0 & 1\end{bmatrix}\begin{bmatrix} angle \\ Q\_bias\end{bmatrix}+\begin{bmatrix}dt \\0\end{bmatrix}newGyro(newGyro在此过程噪声包含于加速度计测量值)\\代码计算\Rightarrow \begin{cases}angle = angle - Q\_bias \cdot dt + newGyro \cdot dt\\Q\_bias = Q\_bias\end{cases}$
  • 预测协方差矩阵
    • $由误差协方差方程P(k|k-1) = AP(k-1|k-1)A^{T} + Q$
    • $先验估计的系统参数A = \begin{bmatrix}1 & -dt \\0 &1\end{bmatrix}$
    • $得出系统过程协方差噪声Q定义\begin{vmatrix}cov(angle, angle) & cov(angle, Q\_bias) \\cov(Q\_bias, andle) & cov(Q\_bias, Q\_bias)\end{vmatrix} \\ 角度噪声和角速度漂移噪声独立，所以\Rightarrow \begin{vmatrix} D(angle) & 0\\ 0 & D(Q\_bias)\end{vmatrix}，\\其中D(angle) = Q\_angle，D(Q\_bias) = Q\_gyro，Q\_angle和Q\_gyro的方差为常数，可由经验给出，或计算得出$
    • 已知Q和A了，怎么得出协方差方程？
      • 设上一次预测协方差矩阵P_k-1为 $\begin{vmatrix}a_{k-1}^{*} & b_{k-1}^{*}\\c_{k-1}^{*} & d_{k-1}^{*}\end{vmatrix}$
      • 本次预测协方差矩阵P_k为 $\begin{vmatrix}a_{k} & b_{k} \\c_{k} & d_{k} \end{vmatrix}$
      • 代入预测里面的协方差公式
        • $\begin{vmatrix}a_{k} & b_{k} \\c_{k} & d_{k} \end{vmatrix} = \begin{bmatrix}1 & -dt \\0 &1\end{bmatrix}\begin{vmatrix}a_{k-1}^{*} & b_{k-1}^{*}\\c_{k-1}^{*} & d_{k-1}^{*}\end{vmatrix}\begin{bmatrix}1 & 0\\-dt &1\end{bmatrix} + \begin{vmatrix} D(angle) & 0\\ 0 & D(Q\_gyro)\end{vmatrix} \\ \Rightarrow \begin{vmatrix}a_{k} & b_{k} \\c_{k} & d_{k} \end{vmatrix} = \begin{vmatrix}a_{k-1}^{*} - c_{k-1}^{*}\cdot dt - b_{k-1}^{*} \cdot dt + d_{k-1}^{*}(dt)^{2} & b_{k-1}^{*} - d_{k-1}^{*}\cdot dt \\c_{k-1}^{*} - d_{k-1}^{*}\cdot dt & d_{k-1}^{*}\end{vmatrix} + \begin{vmatrix} D(angle) & 0\\ 0 & D(Q\_gyro)\end{vmatrix}$
      • 代码：P为2x2矩阵
        • $a_{k} 即为 P[0][0] = P[0][0] + Q\_angle - (P[0][1] + P[1][0]) *dt + P[1][1] * (dt)^{2}，由于dt^{2}太小，比如1ms，P[1][1]项可忽略$
        • $b_{k} 即为 P[0][1] = P[0][1] - P[1][1]*dt$
        • $c_{k} 即为 P[1][0] = P[1][0] - P[1][1]*dt$
        • $d_{k} 即为 P[1][1] = P[1][1] + Q\_gyro$
    • 
    • 
    • 
• 初始化参数：Q,R,P0,x0
• 代入公式迭代
• 调节超参数：Q,R，需要多次人工调节

视频目标跟踪器

选择状态量，观测量

• 状态方程

  $x_{k} = Ax_{k-1} + Bu_{k-1} + w_{k-1}$

  • 状态量 $X = [x, y, w, h, dx, dy]^{T}$
    • x：box中心点的x坐标
    • y：box中心点的y坐标
    • w：box宽
    • h：box高
    • dx：中心点x坐标变化量(速度)
    • dy：中心点y坐标变化量(速度)
  • 状态转移矩阵 A $\begin{bmatrix} 1 & 0 & 0& 0 &1 &0\\ 0 & 1 & 0& 0 &0 &1 \\ 0 & 0 & 1& 0 &0 &0 \\ 0 & 0 & 0& 1 &0 &0 \\ 0 & 0 & 0& 0 &1 &0 \\ 0 & 0 & 0& 0 &0 &1 \\\end{bmatrix}$
  • 控制输入矩阵B=0(零矩阵)
  • 过程噪声：来自于目标移动的不确定性(突然加速、减速、转弯等) $p(w) \sim N(0, Q)$

• 观测方程 $z_{k} = Hx_{k} + v_{k}$

  • t时刻的最优估计值与t+1时刻所有框，IOU最大的，最为t+1时刻的观测值
  • 得到所有观测值x, y, w, h, dx, dy
    • dx = x - x^-(当前时刻 - 上一时刻)
    • dy = y - y^-(当前时刻 - 上一时刻)
  • 状态观测矩阵H=E $\begin{bmatrix} 1 & 0 & 0& 0 &0 &0\\ 0 & 1 & 0& 0 &0 &0 \\ 0 & 0 & 1& 0 &0 &0 \\ 0 & 0 & 0& 1 &0 &0 \\ 0 & 0 & 0& 0 &1 &0 \\ 0 & 0 & 0& 0 &0 &1 \\\end{bmatrix}$
  • 观测噪声：来自于检测框丢失、重叠、不准确等 $p(v) \sim N(0, R)$
  • 如果IOU匹配失败，使用上一次的最优估计值直接作为观测值 $x_{k} = Ax_{k-1}$
    • 此时每帧更新一次状态，直到在t+n帧找到匹配框

代码请看